
For many GMAT test takers, Data Sufficiency questions are the most difficult questions on the GMAT. But what do the hardest GMAT Data Sufficiency questions look like? What skills and concepts do they test? What do they have in common? What Data Sufficiency strategies can we use to get these challenging GMAT Quantitative questions right?
In this article, I’ll go over the five hardest GMAT Data Sufficiency questions, what you’ll need to know to solve them, how to approach them on test day, and what we can learn from hard GMAT Quant questions about mastering Data Sufficiency.
How We Found These GMAT Data Sufficiency Questions
To gather the hardest GMAT questions, our GMAT experts took advantage of the computer adaptive algorithm used on the test. Over the course of the test, the difficulty levels of questions change based on how well you performed on previous questions. Get a few questions right, move up a difficulty level. Get a few questions wrong, move down a difficulty level. By the end of the test, every test taker should be presented with questions that perfectly match their ability.
Our GMAT experts took the practice tests on the GMATPrep software multiple times without missing a single question on the Quantitative section. We collected the questions they received into a master list of the hardest GMAT Quantitative questions. We then looked at activity on various online forums to determine which of these hard GMAT math questions test takers struggled with the most from each question type. This left us with the five hardest GMAT Data Sufficiency questions out there, ready for you to study!
GMAT Data Sufficiency Question 1
The points $A$,$B$,$C$, and $D$ are on a number line, not necessarily in that order. If the distance between $A$ and $B$ is 18 and the distance between $C$ and $D$ is 8, what is the distance between $B$ and $D$?
Not sure how or what to study? Confused by how to improve your score in the shortest time possible? We've created the only Online GMAT Prep Program that identifies your strengths and weaknesses, customizes a study plan, coaches you through lessons and quizzes, and adapts your study plan as you improve.
We believe PrepScholar GMAT is the best GMAT prep program available, especially if you find it hard to organize your study schedule and don't want to spend a ton of money on the other companies' one-size-fits-all study plans.

- The distance between $C$ and $A$ is the same as the distance between $C$ and $B$.
- $A$ is to the left of $D$ on the number line.
- Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- EACH statement ALONE is sufficient.
- Statements (1) and (2) TOGETHER are NOT sufficient.
This particular problem gives us four different numbers on a number line ($A$, $B$, $C$, and $D$) and tells us the distance between two sets of points ($A$ ↔ $B$ and $C$ ↔ $D$). We should also note that these points are not necessarily in alphabetical order. Whenever we have GMAT Quant questions dealing with shapes, graphs, number lines, etc., it’s a really good call to draw out examples — this is the visual equivalent of plugging in numbers.) Applying this trick here, and remembering that the distance between $A$ and $B$ is longer than between $C$ and $D$, we see that our line could look like this:
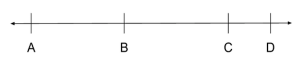 this:
this:
 this:
this:
 and so on.
and so on.
We need to find the distance between $B$ and $D$. This means that we need to gather information
- about the order of the points
- about how our first set of points ($A$ and $B$) relate to our second set of points ($C$ and $D$)
Statement 1
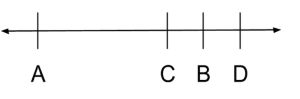
If $A$ and $B$ are two different points and are both the same distance from $C$, this means that the distance between $A$ and $C$ must also be 18 and that $C$ must be directly between the two points like so:
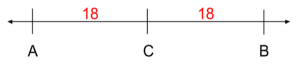 We also know that $D$ is only 8 away from $C$, so it is closer to $C$ than either $A$ or $B$. However, we still don’t know where $D$ is compared to these points. It could be between points $A$ and $C$, making it 26 away from $B$:
We also know that $D$ is only 8 away from $C$, so it is closer to $C$ than either $A$ or $B$. However, we still don’t know where $D$ is compared to these points. It could be between points $A$ and $C$, making it 26 away from $B$:
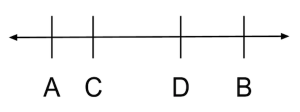
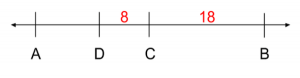 or between points $C$ and $B$, making it 10 away from $B$:
or between points $C$ and $B$, making it 10 away from $B$:
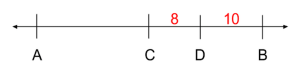 Since we don’t know whether the distance between $B$ and $D$ is 26 or 10, Statement 1 is insufficient.
Since we don’t know whether the distance between $B$ and $D$ is 26 or 10, Statement 1 is insufficient.
Statement 2
Statement 2 tells us that $A$ is to the left of $D$. Well, $A$ is to the left of $D$ in both of the number lines above, and the distance between $B$ and $D$ is not the same in either. So this doesn’t tell us much. If the statement told us that $A$ was directly to the left of $D$, this might be a little more helpful … but it didn’t and it isn’t. Statement 2 is insufficient.
BOTH
Well, we already established that $A$ is to the left of $D$ (fulfilling Statement 2) in both of the number lines we created to fulfilling Statement 1, so even with the information from both statements, we don’t know whether the distance between $B$ and $D$ is 26 or 10. Since we still can’t solve for a single solution, the correct answer is E: Statements 1 and 2 TOGETHER are NOT sufficient to answer the question.

GMAT Data Sufficiency Question 2
If Bob produces 36 or fewer items in a week, he is paid $x$ dollars per item. If Bob produces more than 36 items in a week, he is paid $x$ dollars per item for the first 36 items and $1{1/2}$ times that amount for each additional item. How many items did Bob produce last week?
- Last week Bob was paid a total of \$480 for the items that he produced that week.
- This week Bob produced 2 items more than last week and was paid a total of \$510 for the items that he produced this week.
- Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- EACH statement ALONE is sufficient.
- Statements (1) and (2) TOGETHER are NOT sufficient.
Whenever we have a word problem, like this one, we want to translate the words into math. Scanning over the problem, we see the phrases “36 or fewer” and “more than 36” — these are classic signs that we’re dealing with inequalities. This particular problem gives us two scenarios for calculating how much Bob is paid based on how many total items he produces in a given week (one for 36 or fewer items, one for more than 36 items), so we want to create two equations: one for each scenario. Letting $i$ = the number of items Bob makes in a given week, we can translate our first scenario as
$\If i ≤ 36\, \then \total \pay=x×i$
Our second sentence is a little more complicated. If Bob produces more than Bob is paid $x$ for the first 36 items (or $36x$). Then for all of the items after 36 (or $i-36$), he is paid $1.5x$ (or $1.5x×(i-36)$). Putting that together,
$\If i > 36\, \then \total \pay=x×36 + 1.5x×(i-36)$
So we have two equations, each with three variables ($i$, $x$, and $\total \pay$) … which means we need a bunch of information to figure out an answer. To figure out a value for $i$, we need information about
- which of the two equations to use
- the value of $x$
- the total pay
Statement 1
This statement tells us how much Bob was paid last week, but it doesn’t tell us anything about the specific value of $x$ or which of the two equations we should use. So we could have:
$i=1 \and x=480 → 480=480×1$
or
$i=32 \and x=15 → 480=15×32$
or
$i=76\ \and x=5 → 480=5×36 + 1.5(5)×(40)$
and so on. Statement 1 is insufficient.
Statement 2
This one tells us how much Bob was paid this week, and it compares the number of items he produced this week to the number he produced last week. Well, we don’t know anything about how many items Bob produced last week, so the last piece of information doesn’t tell us much about $x$ — he could have produced 1 item last week and 3 this week or 100 items last week and 102 this week. And, like in Statement 1, we don’t know whether or not $i$ is greater than 36, so we don’t know which statement to use. So we could have:
$i=4 \and x=145 → 580=145×4$
or
$i=29 \and x=20 → 580=20×29$
or
$i=41\, \and x=13{1/3} → 580=13{1/3}×36 + 1.5(13{1/3})×(5)$
and so on. Statement 2 is insufficient.
BOTH
What if we put the two statements together? Well, now we know something: the additional two items Bob produced this week earned him \$30 more than he earned last week. This means that Bob earned an extra /$15 per item. But we’re still missing a key piece of information: which scenario are we dealing with?
- Did Bob produce 36 or fewer items this week? If so, then both items were produced at a rate of $x$, so that $x=15$.
- Did Bob produce at least 38 items this week? If so, then both items were produced at a rate of $1.5x$, so that $1.5x=15$ → $x=10$?
- OR did Bob produce exactly 35 items last week and 37 items this week? If so, then the first item was produced at a rate of $x$ and the second item was produced at a rate of $1.5x$, so that $x+1.5x=30$ → $2.5x=30$ → $x=12$.
We’ve got a few options here, so let’s try each individually. Remember, we want to solve for the number of items Bob produced last week, so we’ll use that equation:
- $x=15$, $480=15i$ → $i=32$
- $x=10$, $480=36(10)+1.5(10)(36-i)$ → $480=360+15(36-i)$ → $120=15(i-36)$ → $8=i-36$ → $i=44$
We already have two possible solutions, so we don’t need to look at our third, more complicated option. We cannot determine whether Bob made 32 or 44 items last week, so we cannot solve the problem with both statements. The correct answer is E: Statements 1 and 2 TOGETHER are NOT sufficient to answer the question.

GMAT Data Sufficiency Question 3
Of the 75 houses in a certain community, 48 have a patio. How many of the houses in the community have a swimming pool?
Want to improve your GMAT score by 60 points?
We have the industry's leading GMAT prep program. Built by Harvard, MIT, Stanford, and Wharton alumni and GMAT 99th percentile scorers, the program learns your strengths and weaknesses and customizes a curriculum so you get the most effective prep possible.

- 38 of the houses in the community have a patio but do not have a swimming pool.
- The number of houses in the community that have a patio and a swimming pool is equal to the number of houses in the community that have neither a swimming pool nor a patio.
- Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- EACH statement ALONE is sufficient.
- Statements (1) and (2) TOGETHER are NOT sufficient.
Reading through the question, we see that we’re dealing with a group of houses where some have a swimming pool and some have a patio. Scanning over the statements, we see that some houses have only a pool, some houses have only a patio, some have neither, and some have both. Almost anytime we see the word “both” in GMAT Quant questions, we’re dealing with an overlapping sets problem — we are looking at two criteria (here, having a pool and having a patio) and where they overlap (here, having “both” a pool and a patio).
Overlapping sets problems have a lot of information, so it’s really easy to get lost in them. A good trick is to use a visual representation to keep track of what you know:
- For two overlapping criteria, use a table, where each axis represents one criterion.
- For three overlapping criteria, use a venn diagram, where each circle represents a criterion.
Here, we have two overlapping sets, so we’re going to use a table. We’ll go ahead and fill in only what was stated directly in the question. We want to find the total number of houses that have a Pool, so we’ll represent that in our table as $x$:
| Patio | No Patio | Total | |
| Pool | $x$ | ||
| No Pool | |||
| Total | 48 | 75 |
Because of the way we’ve set the table up, the two numbers in each row should add up to the total at the end of the row and the two numbers in each columns should add up to the total at the bottom of the column. This means that if we have at least two of the three values in each row or column, we should be able to solve for the third. Looking at our table, we see that our total row along the bottom has two values. If there are 75 houses in total and 48 of those houses have patios, 75 – 48 = 27 of those houses must not have patios. We can go ahead and fill that information in our table:
| Patio | No Patio | Total | |
| Pool | $x$ | ||
| No Pool | |||
| Total | 48 | 27 | 75 |
Doesn’t seem like we can get much more out of our table at this point, so we’ll move on to our Statements.
Statement 1
To start we’ll fill in the information directly given in the statement:
| Patio | No Patio | Total | |
| Pool | $x$ | ||
| No Pool | 38 | ||
| Total | 48 | 27 | 75 |
We see that our first column has two values, so we should be able to solve for the third. If there are 58 houses with patios and 38 of those houses do not have pools, 48 – 38 = 10 of those houses must have pools:
| Patio | No Patio | Total | |
| Pool | 10 | $x$ | |
| No Pool | 38 | ||
| Total | 48 | 27 | 75 |
Looking at the row and the column that contain $x$, we see that we only have one number value for each, meaning that we can’t solve for $x$. Statement 1 is insufficient.
Statement 2
This statement doesn’t give us any concrete numbers to work with, but it does tell us that two of our values (houses with both pools and patios and houses with neither pools nor patios) are equal to each other. When we know that the same number shows up in two places, but we don’t know what that number is, it’s a good idea to represent that number with a variable — if we represent both values as, say, $n$, we know that they are the same number and can combine or eliminate them down the line:
| Patio | No Patio | Total | |
| Pool | $n$ | $x$ | |
| No Pool | $n$ | ||
| Total | 48 | 27 | 75 |
Now we’re getting somewhere! We don’t have two number values in any row or column, but we can use both the top row and the second column to represent No Patio/Pool with variables: if there are $x$ total houses with pools and $n$ of those houses have patios, $x-n$ must not have patios, and if there are 27 total houses that do not have patios, and $n$ of those houses do not have pools, $27-n$ must have pools:
| Patio | No Patio | Total | |
| Pool | $n$ | $x-n$ or $27-n$ | $x$ |
| No Pool | $n$ | ||
| Total | 48 | 27 | 75 |
Since the number of houses with no patio and a pool equals both $x-n$ and $27-n$, we can set the two equal to each other to solve for $x$:
$x-n=27-n$
$x=27$
We were able to determine that 27 houses have pools, which means that Statement 2 is sufficient. The correct answer is B: Statement 2 alone is sufficient to answer the question.

GMAT Data Sufficiency Question 4
Each employee of Company Z is an employee of either Division X or Division Y, but not both. If each division has some part-time employees, is the ratio of the number of full-time employees to the number of part-time employees greater for Division X than for Company Z?
- The ratio of the number of full-time employees to the number of part-time employees is less for Division Y than for Company Z.
- More than half of the full-time employees of Company Z are employees of Division X, and more than half of the the part-time employees of Company Z are employees of Division Y.
- Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- EACH statement ALONE is sufficient.
- Statements (1) and (2) TOGETHER are NOT sufficient.
Right away, the word “ratio” tips us off that we’re dealing with ratios in this problem, and the word “greater” indicates that we’re dealing with inequalities. However, as we read through the rest of the problem, things start to get a little more confusing: one company, two divisions, full-time and part-time employees … this is a lot to process.
We do see the words “either” and “both” though, which should get some overlapping sets wheels turning in our minds. We see that, like the problem above, we have two criteria: employees can belong to Division X or Division Y and can be full-time or part-time. Since this problem doesn’t have any concrete numbers, it isn’t strictly necessary to make a table like we did in the problem above. However, it can still be helpful to define the relationships between our sets and build equations:
| Division X | Division Y | Total (Company Z) | |
| Full-Time | |||
| Part-Time | |||
| Total (employees) |
We know that the two numbers in each row should add up to the total at the end of the row and the two numbers in each columns should add up to the total at the bottom of the column. So we can now build 6 different equations:
- $\Full\-\Time \@ \X + \Part\-\Time \@ \X = \Employees \@ \X$
- $\Full\-\Time \@ \Y + \Part\-\Time \@ \Y = \Employees \@ \Y$
- $\Full\-\Time \@ \Z + \Part\-\Time \@ \Z = \Employees \@ \Z$
- $\Full\-\Time \@ \X + \Full\-\Time \@ \Y = \Full\-\Time \@ \Z$
- $\Part\-\Time \@ \X + \Part\-\Time \@ \Y = \Part\-\Time \@ \Z$
- $\Employees \@ \X + \Employees \@ \Y = \Employees \@ \Z$
Now that we have this set up, let’s figure out what the question is asking for. Like with all word problems, we want to translate words into math. Whenever we’re dealing with ratios, we should remember that ratios can (and should) be expressed as fractions:
Is ${\full\-\time \@ \X}/{\part\-\time \@ \X} > {\full\-\time \@ \Z}/{\part\-\time \@ \Z}$?
or in other words, are there more full-time employees for every part-time employee at Division X than at the entire company?
Statement 1
This Statement gives us information about the ratio of full-time employees to part-time employees at Division Y compared to Company Z:
Want to Identify YOUR GMAT Strengths and Weaknesses?
Our proprietary GMAT Diagnostic Assessment creates a customized study plan for you that takes you from registration all the way to test day! It is included with every account and proven to significantly maximize your score.
Get your personalized assessment as part of your 5 day risk-free trial now:

${\full\-\time \@ \Y}/{\part\-\time \@ \Y} < {\full\-\time \@ \Z}/{\part\-\time \@ \Z}$
Now, before we rule this statement out because it doesn’t tell us anything about Company X, let’s see how we can use our equations to substitute X back into the inequality. Looking at equations 4 and 5, we see that we can rearrange the equations to give:
- $\Full\-\Time \@ \Y = \Full\-\Time \@ \Z – \Full\-\Time \@ \X$
- $\Part\-\Time \@ \Y = \Part\-\Time \@ \Z – \Part\-\Time \@ \X$
Subbing those into our inequality gives us:
${\full\-\time \@ \Z – \full\-\time \@ \X}/{\part\-\time \@ \Z – \part\-\time \@ \X} < {\full\-\time \@ \Z}/{\part\-\time \@ \Z}$
Let’s think about what we know about fractions. To make a fraction smaller, we need to either
- decrease the numerator relative to the denominator
- increase the denominator relative to the numerator
We know that we are decreasing both the numerator and denominator, so we must be decreasing the numerator by a greater percentage than we are decreasing the denominator. This means that the number of full-time employees at Division X is larger relative to the number of part-time employees at Division X than the number of full-time employees at Company Z to the number of part-time employees at Company Z. In other words, the ratio of the number of full-time employees to the number of part-time employees is greater for Division X than for Company Z. Statement 1 is sufficient.
Statement 2
Like with Statement 1, let’s translate this into math:
$\full\-\time \@ \X > {1/2}\full\-\time \@ \Z$
$\part\-\time \@ \Y > {1/2}\part\-\time \@ \Z$
Given equation 5, the second half of our statement also tells us that
$\part\-\time \@ \X < {1/2}\part\-\time \@ \Z$
This means we can write the ratio of full-time employees at Division X as
${>{1/2}\full\-\time \@ \Z}/{<{1/2}\part\-\time \@ \Z}$
or, cancelling the {1/2} in both the numerator and denominator,
${>\full\-\time \@ \Z}/{<\part\-\time \@ \Z}$
To make a fraction larger, we need to either:
- increase the numerator relative to the denominator
- decrease the denominator relative to the numerator
Here, we’re doing both: full-time employees at Division X is greater than full-time employees at Company Z and part-time employees at Division X is less than part-time employees at Company Z. This means that
${\full\-\time \@ \X}/{\part\-\time \@ \X} > {\full\-\time \@ \Z}/{\part\-\time \@ \Z}$
which is exactly what we’re trying to solve for. Statement 2 is sufficient.
Since both statements are sufficient to solve the problem individually, the correct answer is D.

GMAT Data Sufficiency Question 5
If $n$ is a positive integer and $r$ is the remainder when $(n-1)(n+1)$ is divided by 24, what is the value of $r$?
- $n$ is not divisible by 2
- $n$ is not divisible by 3
- Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- EACH statement ALONE is sufficient.
- Statements (1) and (2) TOGETHER are NOT sufficient.
The word “remainder” tells us that we’re dealing with, what else, a remainder problem. Remainder problems scare a lot of students because they don’t involve an easy to use/memorize formula. However, this means that we have a great opportunity to plug in numbers.
Even though this isn’t technically a “word problem”, we still need to translate the words into math to build an equation:
${(n-1)(n+1)}/24 = \? \| \R\: r$
Let’s make a note that $n$ must be a positive integer and move on to our statements.
Statement I
This statement tells us that $n$ is not divisible by two — in other words, it’s telling us that $n$ is odd. Let’s try plugging in numbers. When we select numbers to plug in, our goal is to prove that the statement is insufficient: in other words, we want to pick numbers that will give us different results. We also want to pick numbers that are easy to work with to save time.
We see that one of the values in our numerator is (n-1), which means that picking 1 will give us a zero in our numerator. That seems like it’ll give us an interesting result, so we’ll give it a shot:
${(1-1)(1+1)}/24$
${(0)(2)}/24$
$0/24$
$0 | \R\: 0$
So when $n=1$, $r=0$. Let’s try our next odd number up, $3$ — based on the size of the denominator, it seems like our numerator will be smaller than the denominator, giving a solution of 0 with positive remainder:
${(3-1)(3+1)}/24$
${(2)(4)}/24$
$8/24$
$0 | \R\: 8$
So when $n=3$, $r=8$. This means that $r$ can be either 0 or 8 given Statement 1. Since we can’t find a single value for $r$, Statement 1 is insufficient.
Statement II
This statement tells us that $n$ is not divisible by three. That knocks $n=3$ out of the running. $n=1$ still works, however, so we know that $r=0$ is still a possibility given Statement 2.
Since we tried only odd numbers last time, let’s try an even number this time to see if that changes things up: we’ll do 2 to keep our numbers easy to work with:
${(2-1)(2+1)}/24$
${(1)(3)}/24$
$3/24$
$0 | \R\: 3$
So when $n=2$, $r=3$. This means that $r$ can be either 0 or 3 given Statement 2. Like before, since we can’t find a single value for $r$, Statement 2 is insufficient.
BOTH
Putting these two statements together, we know that $n$ must be odd and cannot be divisible by 3: so we have 1, 5, 7, 11, etc. These numbers are going to get pretty big pretty fast, so let’s try them from smallest to greatest. We already know that $r=0$ when $n=1$, so we want to find a positive value for $r$ to prove that both statements are insufficient:
${(5-1)(5+1)}/24$
${(4)(6)}/24$
$24/24$
$1 | \R\: 0$
So when $n=5$, $r=0$. That’s the same as when $n=1$. Let’s try the next number up, 7:
${(7-1)(7+1)}/24$
${(6)(8)}/24$
$48/24$
$2 | \R\: 0$
So when $n=7$, $r=0$. We’re starting to see the hints of a pattern here. Let’s try one more, 11, to be sure:
${(11-1)(11+1)}/24$
${(10)(12)}/24$
$120/24$
$5 | \R\: 0$
So when $n=7$, $r=0$. Once we’ve tried at least 4 numbers in a series and confirmed that we’ve done a reasonable job picking numbers that would give us different results, we can usually determine that we have a pattern. Here, we can say confidently that given Statement 1 and Statement 2, $r$ will always be 0. This means that the correct answer is C: BOTH statements together are sufficient.

Key Takeaways: Learning From The Hardest Data Sufficiency Questions
So what can the hardest GMAT Quantitative questions teach us about GMAT Data Sufficiency questions in general?
- Visuals — drawings, tables, Venn diagrams, graphs, what have you — are our friends, and not only on Geometry questions. On the GMAT, advanced quant questions are hard to conceptualize, and drawing things out keeps us from having to keep track of a lot of complicated relationships in our heads.
- Whenever we have words, we need to translate them into math. Like visuals, building equations helps us take hard GMAT math questions and distill them into something we can work with. Use math-y keywords, like “greater than”, “equal to”, “divided by”, etc. to break sentences down into their component parts.
- The hardest GMAT Data Sufficiency questions often involve more logic than simple math, especially around number sense concepts. Being comfortable making inferences based on what we know can save us a lot of time compared to slogging through a bunch of proofs.
- That said, picking numbers to plug in is a great Data Sufficiency strategy that can help us avoid overthinking a problem or confirm our logic. Always pick numbers that you think will yield two different solutions, making the statement insufficient.
What’s Next?
What are the math concepts tested on the GMAT? The best GMAT math tricks and shortcuts? The most important Data Sufficiency tips? These articles expand on the concepts used in these five problems, explaining what you need to know about GMAT Data Sufficiency before test day.
Looking to improve your Quant score? This article explains what exactly a good GMAT Quantitative score is.
If you’d like similar analyses of the hardest questions from other GMAT question types, check out our post on the five hardest Sentence Correction questions.
 PrepScholar GMAT
PrepScholar GMAT