
If you’re like me, you probably spent a lot of time in high school memorizing the difference between sine and cosine and sighing over long, multi-step proofs, only to forget all of this hard-earned knowledge the second that classes dismissed for break.
If you’ve forgotten a lot of your high school geometry rules or are just in need of a refresher before taking the GMAT, then you’ve found the right article. In this article, I’ll be giving you a comprehensive overview of GMAT geometry.
First, I’ll talk about what and how much geometry is actually on the GMAT. Next, I’ll give you an overview of the most important GMAT geometry formulas and rules you need to know. Then, I’ll show you four geometry sample questions and explain how to solve them. Finally, I’ll talk about how to study for the geometry you’ll encounter on the GMAT and give you tips for acing test day.
GMAT Geometry: What to Expect
If you feel like you’ve forgotten a lot of the geometry that you learned in high school, don’t worry. The GMAT only covers a fraction of the geometry that you probably studied in high school. In the next section, I’ll talk about the geometry concepts that you’ll actually find on the GMAT.
You’ll find geometry concepts in both data sufficiency and problem-solving questions. Geometry questions make up just under a quarter of all questions on the GMAT quant section. As with all GMAT quant questions, you won’t just need to know how to apply geometry principles in isolation. You’ll need to know how to combine your geometry knowledge with knowledge of other concepts (like number properties, for instance) to get at the correct answer. I’ll talk more about what this actually means when I go over some geometry sample questions.
Not sure how or what to study? Confused by how to improve your score in the shortest time possible? We've created the only Online GMAT Prep Program that identifies your strengths and weaknesses, customizes a study plan, coaches you through lessons and quizzes, and adapts your study plan as you improve.
We believe PrepScholar GMAT is the best GMAT prep program available, especially if you find it hard to organize your study schedule and don't want to spend a ton of money on the other companies' one-size-fits-all study plans.

As I mentioned before, the GMAT only covers a fraction of the geometry that you learned in high school. As with the rest of the content on the GMAT Quant section, you’ll only need to know how to apply high school geometry concepts, which may be a relief to some test-takers.
Unfortunately, unlike some other standardized tests (like the SAT), the GMAT doesn’t provide any formulas for you. You’ll have to memorize all the formulas and rules you’ll need to know for the test.
In the next section, I’ll talk to you about the most important rules and formulas you’ll need to know to answer geometry problem solving and data sufficiency questions.

The Most Important GMAT Geometry Formulas and Rules to Know
The good news about GMAT geometry is that you don’t need to brush up on a whole bunch of topics in order to do well. The bad news about GMAT geometry is that you’ll have to memorize all the rules and formulas you need to know for the test, because none will be provided to you on test day. You also can’t bring in any aids to help you with the exam.
In this section, I’ll talk about the major GMAT geometry formulas and rules that you should study and memorize as you’re preparing for the exam.
Lines and Angles
- A line is a one-dimensional abstraction that goes on forever.
- For any two points, there is one straight line (only one!) that passes through them.
- A line section is a segment of a straight line that has two endpoints. The midpoint is the point that divides the line segment into two equal parts.
- Two lines are parallel if they lie in the same plane and never intersect. Two lines are perpendicular if they intersect at a 90° angle.

- An angle is made when two lines intersect at a point. This point is called the vertex of the angle.
- Angles are measured in degrees (°).
- An acute angle is an angle whose degree measure is less then 90°.
- A right angle’s degree measure is exactly 90°.
- An obtuse angle’s degree measure greater than 90°.
- A straight angle’s degree measure is 180°.
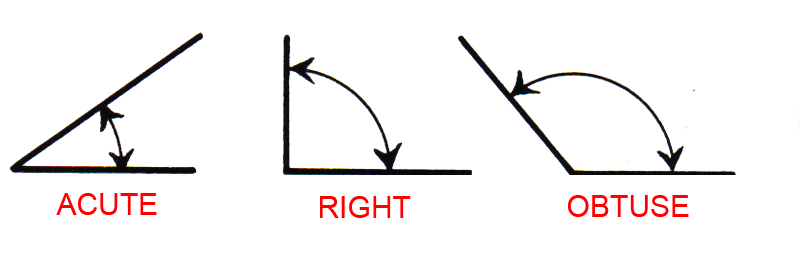
- The sum of the measures of angles on a straight line is 180°.
- The sum of the measures of the angles around a point (which make a circle) is 360°.
- Two angles are supplementary if their sums make a straight angle.
- Two angles are complementary if their sums make a right angle.
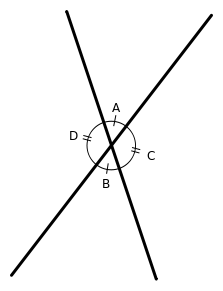
- Vertical angles are opposite angles formed by two intersecting line segments.
- A line or a segment bisects an angle if it splits the angle into two, smaller equal angles.
- Vertical angles are a pair of opposite angles formed by intersecting line angles. The two angles in a pair of vertical angles have the same degree measure.
Triangles
- A triangle is a closed figure with three angles and three straight sides.
- The sum of the interior angles of a triangle is 180°.
- Each interior angle is supplementary to an adjacent exterior angle. Together, they equal 180°.
- The formula for finding the area of a triangle is $½bh$.
- $b$ = base
- $h$ = height
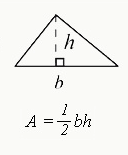
- An isosceles triangle has two sides of equal length.
- An equilateral triangle has three equal sides and three angles of 60°.
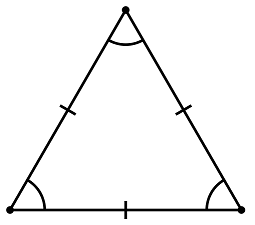
- There are two kinds of special right triangles:
- Isosceles right triangles have a side relationship of 1:1:$√2$.
- 30°60°90° triangles have a side relationship of 1:$√3$:2.
- A right triangle has one 90° interior angle. The side opposite the right angle is called the hypotenuse and it’s the longest side of the triangle.
- Pythagorean Theorem for finding side lengths of a right triangle: $a^2 + b^2 = c^2$
- Two triangles are similar if their corresponding angles have the same degree measure.
- Two triangles are congruent if corresponding angles have the same measure and corresponding sides have the same length.
Circles
- The diameter of a circle is a line segment that connects two points on the circle and passes through the center of the circle.
- The radius is a line segment from the center of the circle to any point on it.
- A circle’s central angle is formed by two radii.
- The distance around the circle is called circumference:
- $C=πd$
- $C = 2πr$
- An arc is a part of the circumference of a circle.
- $\Length = (n/360°)C$, where $n$ is the measurement of the central angle of the circle portion in degrees.
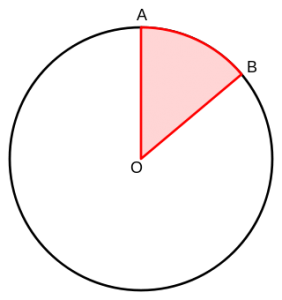
- The area of a circle is found with the formula $A = πr^2$.
Polygons
- A polygon is a closed figure that has straight line segments as its sides.
- The perimeter of a polygon is the distance around the polygon (the sum of the length of all its sides).
- The sum of the four interior angles of a quadrilateral is 360°.
- Area of a square: $s^2$
- Area of a rectangle: $l$$w$
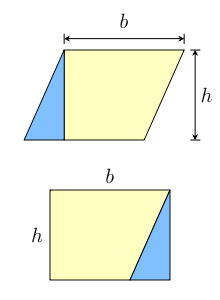
- Area of a parallelogram: $b$$h$
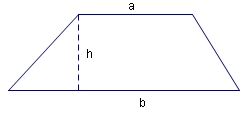
- Area of a trapezoid: $1/2(a + b)h$
Solids
- A cylinder is a solid whose horizontal cross section is a circle.
- Volume of a cylinder: $Bh$, where $B$ is the area of the base.
- Area of the base of a cylinder: ?r2 (because, remember, a cylinder has a circular cross section)
- A cube is a rectangular solid where all the faces are squares.
- Volume of a cube: $Bh$, where $B$ is the area of the base.
- A rectangular solid is a solid with six rectangular faces.
- Volume of a rectangular solid: $lwh$
Want to improve your GMAT score by 60 points?
We have the industry's leading GMAT prep program. Built by Harvard, MIT, Stanford, and Wharton alumni and GMAT 99th percentile scorers, the program learns your strengths and weaknesses and customizes a curriculum so you get the most effective prep possible.

Coordinate Geometry
- The slope of a line tells you how steeply that line goes up or down the coordinate plane.
- $slope$ = $rise$/$run$
- $slope = change in $y$ / change in $x$
- The rise is the difference between the $y$-coordinate values of two points on the line; the run is the difference between the x-coordinate values of two points on the line.
- You can also find the slope of a line using the slope-intercept equation, which is $y = mx + b$, where the slope is $m$ and the $b$ is the value of the $y$-intercept.
- Perpendicular lines have slopes that are negative reciprocals of one another.
- To determine the distance between any two points on a coordinate plane, you can use the Pythagorean theorem.
4 Tips for GMAT Geometry Questions
Even the most prepared test-takers can feel a lot of anxiety on test day. Follow these tips to boost your score and help you work your way through tricky GMAT geometry questions.
#1: Use What You Know
For all GMAT geometry questions, start by identifying what you know and what you need to find out. Use the information in the question and in any diagrams to build up your understanding of a figure. For instance, if you know that the measure of two different angles in a triangle are 60 degrees and 80 degrees, respectively, you can use what you know to figure out the measure of the third angle. The more information you have, the more you’ll be able to figure out.
#2: Look for Connections on Multiple Figure Questions
If there is more than one recognizable shape in a diagram, there is a connection between them. Look for what one of the figures tells you about the other. Perhaps the diagonal of a square is the same as the radius of a circle. Or the height of one triangle is the hypotenuse of another. Whatever the connection, it’s probably the key to answering the question.
#3: Don’t Assume That Drawings Are To Scale
You can’t assume that diagrams on the GMAT are to-scale. If you’re assuming a shape is a square and it’s actually a rectangle, you can make big mistakes in your calculations. Only use the information given to you on the diagram or in the question itself. Don’t ever assume anything that you can’t reason out with cold, hard math.
#4: Make Your Own Diagram
If you’re solving a question that involves a shape, but the test doesn’t give you a diagram, make your own. Making your own diagram will help you better visualize a question. You can also re-draw a diagram on your scrap paper even if the test provides you with a diagram to view. Sometimes, re-drawing a diagram will help you get a better understanding of the figure so that you can more easily solve the problem.
GMAT Geometry Practice Questions
One of the most important parts of preparing for the GMAT is to practice solving real GMAT questions. Solving real GMAT geometry questions helps you prepare for the content that you’ll actually see on the test. In this section, I’ll walk you through four real GMAT sample questions that use geometry concepts: two problem-solving questions and two data sufficiency questions.
Problem Solving Sample Question 1
A rectangular floor that measures 8 meters by 10 meters is to be covered with carpet squares that each measure 2 meters by 2 meters. If the carpet squares cost $12 apiece, what is the total cost for the number of carpet squares needed to cover the floor?
- $200
- $240
- $480
- $960
- $1920
To start, since this problem doesn’t provide a diagram, we want to draw our own on scrap paper. Drawing your own diagram helps you better visualize the problem. So, draw a rectangle and label the sides “8 m” and “10 m,” since we know that from the problem.
Next, let’s take a step back and think about what the question is asking us. It’s asking to figure out the cost of covering a floor in carpet squares. When you’re covering a floor in carpet squares, you want to cover the entire area of the floor. So, our next step is to find the area.
We know that the formula for area of a rectangle is $a = lw$. Let’s solve that using the information we have. $A = (8)(10)$. The area of this rectangle is 80 $m^2$.
Now, we need to figure out how much area each carpet square covers. The formula for finding the area of a square is also $lw$, so let’s go ahead and do that. $Area = (2m)(2m)$. The area covered by each carpet square is 4$m^2$.
To find the number of carpet squares needed to cover the floor, we’ll divide the total area of the floor by the area of each individual carpet square. $80 m^2/ 4 m^2 = 20$ total carpet squares needed to cover the floor.
Want to Identify YOUR GMAT Strengths and Weaknesses?
Our proprietary GMAT Diagnostic Assessment creates a customized study plan for you that takes you from registration all the way to test day! It is included with every account and proven to significantly maximize your score.
Get your personalized assessment as part of your 5 day risk-free trial now:

The cost of each carpet square is 12, so for our final step, we’ll multiply 20 (number of carpet squares needed) by 12 (cost per carpet square) to get a total of $240.
The correct answer is B.
Problem Solving Sample Question 2
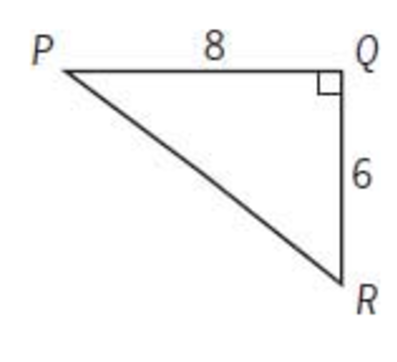 The figure above shows a path around a triangular piece of land. Mary walked the distance of 8 miles from $P$ to $Q$ and then walked the distance of 6 miles from $Q$ to $R$. If Ted walked directly from $P$ to $R$, by what percent did the distance that Mary walked exceed the distance that Ted walked?
The figure above shows a path around a triangular piece of land. Mary walked the distance of 8 miles from $P$ to $Q$ and then walked the distance of 6 miles from $Q$ to $R$. If Ted walked directly from $P$ to $R$, by what percent did the distance that Mary walked exceed the distance that Ted walked?
- 30%
- 40%
- 50%
- 60%
- 80%
As always, let’s start by figuring out what this question’s asking us. It’s asking us to compare the distance Mary walked to the distance Ted walked. In order to do that, we need to first figure out how far they actually walked.
It’s pretty easy to figure out how far Mary walked. We can just add 8 + 6. Mary walked 14 miles.
It’s a little trickier to figure out how far Ted walked. Notice that the diagram is in the shape of a right triangle. That tells us that we can use the Pythagorean theorem to find the length of Ted’s walk, which is really just the missing side of this triangle. Since Ted’s side is across from the right angle, we know that it’s the hypotenuse. Therefore, we can plug in our sides pretty easily. $8^2$ +$6^2$ = $PR^2$ or $64$ + $36$ = $PR^2$, or $100 = $PR^2$. We can then find the square root of 100, which is 10. So, $PR = 10mi$.
Now, we know that Mary walked 14 miles and Ted walked 10 miles. Therefore, the distance Mary walked exceeded the distance Ted walked by 4 miles ($14 – 10 = 4$). 4 is 40% of 10, so the correct answer is B. Mary exceeded the distance Ted walked by 40%.
Data Sufficiency Sample Question 1
 In the figure above, point D is on AC. What is the degree measure of $\angle ∠ {BAC}$?
In the figure above, point D is on AC. What is the degree measure of $\angle ∠ {BAC}$?
- The measure of BDC is 60°.
- The degree measure of BAC is less than the degree measure of $\angle ∠ {BCD}$.
- Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- EACH statement ALONE is sufficient.
- Statements (1) and (2) TOGETHER are NOT sufficient.
This question’s asking us to determine measure of an interior angle of a triangle. For data sufficiency questions, we always want to address each statement separately FIRST. Let’s begin with statement (1).
Statement (1) states that angle BDC measures 60 degrees. Since we know that $\angle ∠ {BDC}$ is on a straight line, we know that the angle adjacent to it ($\angle ∠ {BDA}$) can be added to $\angle ∠ {BDC}$to equal 180°. So, we can find the measure of angle BDA by using the equation: $180 – 60$ = $\angle ∠ {BDA}$. Therefore, we know the measure of $\angle ∠ {BDA}$ is 120°.
Next, we know that all the angles inside a triangle add up to 180°. Since we now know the measure of angle BDA (120) and the measure of $\angle ∠ {ABD}$ (20), we can find the third angle in that triangle by using the equation 180 – (20 + 120) = $\angle ∠ {BAC}$. So, statement (1) is sufficient. We now can eliminate answer B and answer E.
Now, let’s move on to statement (2). We want to forget everything we know about statement (1) at first and address statement (2) by itself.
The statement tells us that the degree measure of $\angle ∠ {BAC}$ is less than the degree measure of $\angle ∠ {BCD}$. However, we don’t have enough information to figure out what the measure of either angle actually is. So, statement (2) is not sufficient.
The correct answer then is A; statement (1) alone is sufficient.
Data Sufficiency Sample Question 2
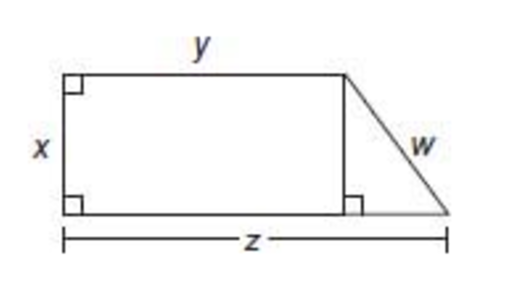 In the figure above, what is the value of $z$?
In the figure above, what is the value of $z$?
- $x = y = 1$
- $w = 2$
- Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- EACH statement ALONE is sufficient.
- Statements (1) and (2) TOGETHER are NOT sufficient.
Remember, when solving data sufficiency questions, you want to take each statement by itself first. Also keep in mind that you can’t assume that any diagrams given are to scale. You might be tempted to say that the triangle pictured is an isosceles right triangle, but you can’t assume that. Keeping all this in mind, let’s look at statement (1).
Statement (1) says that $x = y = 1$. That means that both $x$ and $y$ = 1. Can we use that to find the value of z?
Well, we know that the value of z is equal to 1 + the value of the base of the right triangle. There’s no information in the problem to tell us what the value of the base of the right triangle is. So, the value of the base can vary, so the value of $z$ can vary.
That means that statement (1) isn’t sufficient by itself.
Now, let’s look at statement (2) by itself first. Statement (2) says $w = 2$. However, even though we know that $w = 2$, we don’t know anything about the rest of the sides. That means all the other sides can vary, so z can vary as well. Statement (2) isn’t sufficient by itself either.
Now, let’s look at the two statements together.
Taking (1) and (2) together, we know that $z = y + (z – y)$ [the base of the triangle]. Or, we can say that $z = 1y + (z – 1)$.
The value of $z – 1$ can be determined by applying the Pythagorean theorem to the triangle. We know that the hypotenuse is 2 (from statement (2): $w = 2$) and we know that one side = 1 (from $x = 1$) and one side equals $z – 1$.
We can then write the equation $1^2 + (z – 1)^2 = 2^2$. Since we only have one variable in the equation, we can solve through for z.
You don’t need to solve a data sufficiency question. You only need to know that you can! So since we know we can solve the question using both statements, the correct answer is C. Both statements together are sufficient.

How to Study for Geometry on the GMAT
Studying for the GMAT may seem overwhelming, because there’s a lot of content to review. The good news is that executing a well-thought-out study plan will help you achieve your goals. Here are some tips geometry for the GMAT.
#1: Use High Quality Practice Materials
The best way to prepare for the GMAT is by using real GMAT geometry questions in your prep. Real GMAT geometry questions will simulate the GMAT’s style and content. For instance, you’ll have to use more than one skill in the question, or you’ll get practice using your geometry skills on data sufficiency questions, which are unique to the GMAT. Using resources like GMATPrep or the GMAT Official Guide will give you access to real, retired GMAT questions.
As you might’ve noticed from our practice questions, you’ll rarely see a straightforward question on the GMAT that just asks you to use your geometry skills. You’ll likely have to combine your knowledge of geometry with your knowledge of arithmetic or number properties or ratios… or all of the above! Practicing GMAT-style questions (real, retired GMAT questions if you can get them) will give you practice at using multiple skills in one question.
#2: Memorize Important Formulas
As I mentioned before, you won’t get to use a formula cheat sheet on the GMAT. You’ll have memorize all the formulas you expect to need on test day. Using flashcards is a great way to build your knowledge so that you can quickly recall and use important formulas on test day.
What’s Next?
You’ve read all about the formulas you need to know for GMAT geometry. Are you ready to master them? Using flashcards can be a great way to boost your memory. Before you get started with flashcards, check out our total guide to GMAT flashcards to learn about the best GMAT flashcards out there and the best way to study with flashcards.
Feel like you’ve mastered GMAT geometry? Looking for a new challenge on your quest to total GMAT quant domination? Check out our guide to GMAT probability to conquer a new type of math of the GMAT.
Are you totally confused by the data sufficiency practice questions? If so, don’t worry. Data sufficiency questions may seem strange, but our total guide to data sufficiency on the GMAT will break down everything you need to know to master this question type.
 PrepScholar GMAT
PrepScholar GMAT
