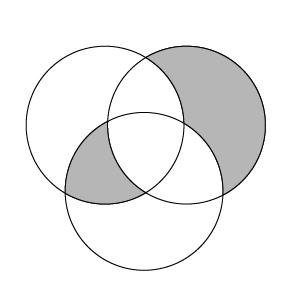
The area of each of the three circular regions in the figure shown is $40$, and the area of the intersection of any two of the circular regions is $15$.
| Quantity A | $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ | Quantity B |
| $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ | ||
| The sum of the areas of the shaded regions | $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ | $30$ |
- Quantity A is greater.
- Quantity B is greater.
- The two quantities are equal.
- The relationship cannot be determined from the information given.
So, you were trying to be a good test taker and practice for the GRE with PowerPrep online. Buuuut then you had some questions about the quant section—specifically question 7 of Section 6 of Practice Test 1. Those questions testing our knowledge of Circles can be kind of tricky, but never fear, PrepScholar has got your back!
Survey the Question
Let’s search the problem for clues as to what it will be testing, as this will help shift our minds to think about what type of math knowledge we’ll use to solve this question. Pay attention to any words that sound math-specific and anything special about what the numbers look like, and mark them on our paper.
Circles on top of circles! Probably tests our knowledge of…Circles. Let’s keep what we’ve learned about this skill at the tip of our minds as we approach this question.
What Do We Know?
Let’s carefully read through the question and make a list of the things that we know.
- The area of each individual circle is $40$
- The area where any two circles intersect is $15$
- We want to find the area of the shaded region shown
Develop a Plan
Ah, shaded regions! One of our favorite geometry questions. While this question might appear to be very difficult at first,
we should keep in mind that most geometry questions involving shaded regions involve either: 1) subtracting one region from another region or 2) finding a clever way to view the shaded region. Let’s see if we can apply one of those two principles to make this question simpler.
Solve the Question
First, let’s take a look again at the figure in the question:

We know that the area of each circle is $40$. We also know that the area of intersection of any two circles is $15$. Unfortunately, these shaded areas aren’t in the same circle. It should be easier if the shaded regions were in the same circle, so let’s see if we can use symmetry to accomplish this.
Hmmm…we do know that these two shaded regions are equal to each other:
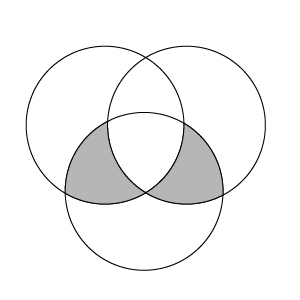
So let’s think about the shaded regions like this:
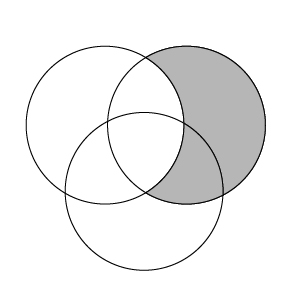
Ah ha! This makes the problem a whole lot easier! Alright, so we know that the area of the circle in the upper-right is $40$. We can now see that our shaded region is the difference between the area of the circle in the upper-right (which we know is $40$) and the intersection of the upper-right and upper-left circles (which we know is $15$). So the area of the shaded region must be $40-15=25$.
Since we now know that Quantity A is $25$, then it is less than Quantity B, which is $30$. The correct answer is B,
Quantity B is greater.
What Did We Learn
This problem became a lot easier once we redrew our figure to move one of the shaded regions to another region with an equivalent area. Let’s always keep our minds flexible when approaching questions involving shaded regions.
Want more expert GRE prep? Sign up for the five-day free trial of our PrepScholar GRE Online Prep Program to access your personalized study plan with 90 interactive lessons and over 1600 GRE questions.
Have questions? Leave a comment or send us an email at [email protected].

