
If you’re worried about the GRE Quant section, you’re not alone. Not everyone taking the GRE is an aspiring engineer or an exceptional mathematician. In fact, many of us are surprised to find we remember little of the basic math concepts we studied back in high school. (When I took the GRE in 2015, I hadn’t studied math in more than six years!)
But Quant really isn’t all that bad, as long as you know what to expect. And it never hurts to have a couple of tricks up your sleeve, either. No, I’m not talking about cheating. Just our handy, dandy GRE formulas!
For this GRE math cheat sheet, I’ll explain why all test takers should memorize GRE math formulas, go over what these formulas are, and give you detailed tips on how to integrate them effectively into your test prep.
Why Should You Memorize Math Formulas?
You might be wondering, “Is it really worth the time to memorize all of these formulas?” And my answer is, absolutely. If scoring well on GRE Quant is a goal of yours (as it is for many GRE takers), memorizing common GRE math formulas gives you a big advantage on test day.
Why? Well, knowing exactly when and how to apply certain formulas means you’ll be answering Quant questions faster and more accurately — resulting in a higher Quant score. And as you might have guessed, a higher Quant score can significantly increase your chance of getting into grad school. Clearly, formulas are a pretty big deal on the GRE!
In fact, GRE math formulas are often the major key to solving certain types of Quant problems. If you can’t recall a specific GRE formula, there’s a strong chance you won’t be able to solve the problem at all without it. As a result, there’s a good possibility you’ll choose the wrong answer choice. And the more incorrect guesses you make, the lower your overall Quant score will be.
At other times, a GRE math formula isn’t an absolute necessity for solving a problem, but knowing it will save you time and complicated calculations. Remember, you should never spend too much time on a single Quant question. If you do, you might fail to finish the test and therefore get a lower score.
Quick side note: we've created the world's leading online GRE prep program that adapts to you and your strengths and weaknesses. Not sure what to study? Confused by how to improve your score? We give you minute by minute guide.
You don't NEED a prep program to get a great GRE score. But we believe PrepScholar is the best GRE prep program available right now, especially if you find it hard to organize your study schedule and don't know what to study.
Click here to learn how you can improve your GRE score by 7 points, guaranteed.
So what kinds of formulas does the GRE use? Are you expected to know calculus and upper-level concepts?
The good news is that the math on Quant isn’t overly difficult. The GRE only tests arithmetic, geometry, algebra, and data analysis (e.g., reading graphs, tables, etc.) — all concepts you studied in middle school and high school. In other words, all GRE math formulas are formulas you learned at some point prior to college.
The bad news, however, is that the GRE likes to trick test takers. Oftentimes, questions are purposely vague. Sometimes, a problem may even give you an important formula, but it’s written in such a way it’s nearly unrecognizable!
Still, the GRE isn’t unbeatable. Once you know the ins and outs of the major formulas tested on Quant, you’ll likely score higher than you ever imagined yourself capable of scoring.
Without further ado, let’s dive into our GRE math cheat sheet!

38 GRE Math Formulas You Must Know
In this section, we’ve aggregated 38 of the most important GRE math formulas you’ll need for tackling Quant head-on. Knowing how they function will ultimately help you score well on Quant — not to mention impress the heck out of your programs!
Geometry
Square
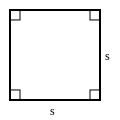
Perimeter
$P=4s$
- Multiply any one side (s) by four.
Area
$A=s^2$
- Multiply any two sides together (i.e., square one side).
Rectangle
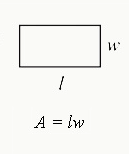
Perimeter
$P=2l+2w$
- Multiply the length (l) by 2 and the width (w) by 2, and then add the products together.
Area
$A=lw$
- Multiply the length by the width.
Circle
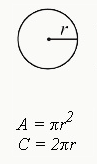
Circumference
$C=2πr$
or
$C=πd$
- Multiply 2, π (pi), and the radius (r) (the length of a line connecting the center of the circle to the edge).
- Alternatively, multiply π by the diameter (d) (the length of a line cutting the circle in half).
- Two radii (the plural of radius) equal the diameter, so $2r=d$.
- π can be rounded to 3.14 (or 3.14159).
Area
$A=πr^2$
- Square the radius and multiply it by π.
- Note: all circles equal 360 degrees.
Triangle
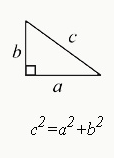 Pythagorean Theorem
Pythagorean Theorem
$a^2+b^2=c^2$
- This theorem can only be used for right triangles (triangles with a 90-degree angle).
- a and b are the two shorter sides, or “legs,” and c is the hypotenuse (the longest side of a right triangle).
- Certain triangle-side combinations (a:b:c), called Pythagorean triples, are easy to memorize. Common ones you may come across on the GRE are:
- 3:4:5
- 5:12:13
- 8:15:17
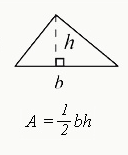
Want to improve your GRE score by 7 points? We have the industry's leading GRE prep program. Built by world-class instructors with 99th percentile GRE scores, the program learns your strengths and weaknesses through machine learning data science, then customizes your prep program to you so you get the most effective prep possible.
Try our 5-day full access trial for free:
Area
$$A={1/2}bh$$
- Multiply the base (b) by the height (h) and divide by 2.
- Note: angles in a triangle always add up to 180 degrees.
Trapezoid
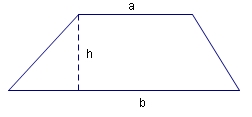
Area
$$A={{a+b}/2}h$$
- a and b are parallel sides.
- Add a and b, divide by 2, and then multiply by the height (h).
Laws of Exponents
$x^0=1$
$x^{-1}=1/x$, $x^{-2}=1/x^2$, etc.
${x^a}{x^b}=x^{a+b}$
$${x^a}/{x^b}=x^(a-b)=1/{x^{b-a}}$$
${x^a}{y^a}=(xy)^a$
$$(x/y)^a={x^a}/{y^a}$$
$(x^a)^b=x^{ab}$
Laws of Square Roots
$√{a^2}=a$
$√a√b=√{ab}$
$$√a/√b=√{a/b}$$
Laws of Even and Odd Numbers
even + even = even
odd + odd = even
even + odd = odd
even * even = even
odd * odd = odd
even * odd = even
Distance
$D=rt$
- Multiply the rate (r) by the time (t) to find the distance (D).
- You can also solve for the time or rate by rearranging this formula to equal either r or t:
$r=D/t$
$t=D/r$
Slope of a Line
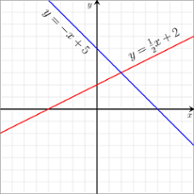
Using the Equation of a Line
$y=mx+b$
- A slope is the steepness of a line in a coordinate system.
- m is the slope.
- x and y are a pair of coordinates.
- b is the y-intercept, or where the line passes through the y-axis.
- You may occasionally see this equation written in a different way (e.g., $b=y-mx$). Always convert it to the format above to ease calculations and avoid confusion.
- A line increasing as it moves left to right has a positive slope, whereas a decreasing line has a negative slope. A completely horizontal line has a slope of 0.
- If the y-intercept of a line is 0, the formula for it is $y=mx+0$, or simply $y=mx$. Here’s an example:

Using Two Sets of Coordinates
Want to improve your GRE score by 7+ points?
Check out our best-in-class online GRE prep program. We guarantee your money back if you don't improve your GRE score by 7 points or more.
PrepScholar GRE is entirely online, and it customizes your prep program to your strengths and weaknesses. We also feature 2,000 practice questions, official practice tests, 150 hours of interactive lessons, and 1-on-1 scoring and feedback on your AWA essays.
Check out our 5-day free trial now:
$$m={y_2-y_1}/{x_2-x_1}$$
or
$$\slope= \rise/ \run$$
- $x_1$ and $y_1$ are a corresponding pair of coordinates on a line. ($x_2$ and $y_2$ are a separate pair of coordinates on the same line.)
- This equation is known as rise over run (the change in vertical distance over the change in horizontal distance).
Average
$$\average={\sum \of n \numbers}/n$$
$${\average \speed}={\total \distance}/{\total \time}$$
- The average is also called the mean.
- Don’t confuse the average for other statistical terms. Common terms you may see on the GRE are:
- Mode: the most common number of a data set
- Range: the difference between the highest number and the lowest number of a data set
- Median: the middle number of a data set
Probability
$${\probability \of \an \event \occurring}={\number \of \successful \outcomes}/{\total \number \of \possible \outcomes}$$
probability of two independent events occurring = probability of event A * probability of event B
- Probabilities are usually written as fractions, though you may see them written as decimals or ratios (e.g., 3:4).
Percentages

Percent Basics
Solve for x percent of number n
$$n{x/100}$$
- Alternatively, a faster way to solve this is by moving the decimal point of the percent to the left two places and multiplying it by n. For example, what is 12 percent of 50? Answer: $50{(0.12)}=6$.
Solve for what number n is x percent of
$${100n}/x$$
Solve for what percent is number n of number m
$${100n}/m$$
Percent Change
Percent Increase
$${{\final \amount – \original \amount}/{\original \amount}}*100$$
- The numerator is equivalent to the actual increase in the amount.
Percent Decrease
$${{\original \amount -\final \amount }/{\original \amount}}*100$$
- The numerator is equivalent to the actual decrease in the amount.

How to Use GRE Math Formulas in Your Test Prep
Our GRE math cheat sheet above covers the 38 most important GRE formulas. But how exactly should you study these? Here are three ideas for getting to know these formulas inside and out.
#1: Make Flashcards
Some of you readers skimming this GRE cheat sheet are probably thinking, “How on earth am I supposed to memorize all of these?!” Well, it’s not as difficult as it looks. As long as you’re a fan of flashcards.
That’s right — the easiest way to memorize GRE formulas (and Verbal vocab, too) is by creating your own set of flashcards. This way, you’ll have complete control over what you study.
To make paper flashcards, write a GRE math formula on one side of a note card, and what and how it’s used on the other side. You’ll also want to note what each of the terms in a formula means (e.g., the m in the slope formula is the slope). If you have extra room, draw a diagram or two to illustrate what the formula looks like.
You can also try creating your own set of digital flashcards. Most digital decks these days use spaced-repetition software (SRS) to show you difficult flashcards more often than the flashcards you already know. I recommend downloading a free software called Anki to get a feel for how the system works. With Anki, you can make your own flashcards, download shared decks, and study completely offline. It’s a pretty convenient system, especially if you’re prone to losing paper flashcards (like me).

#2: Familiarize Yourself With How They’re Tested
Understanding how the major GRE math formulas are tested on the GRE is important because it provides you with a clear and accurate vision of what to expect on test day.
To start, the GRE Quant section is composed of four types of questions:
- Quantitative Comparison (or “Quant Comp” for short): asks you to compare two quantities
- Multiple Choice (select one answer): asks you to choose a single answer choice
- Multiple Choice (select one or more answers): asks you to choose one or several answer choices
- Numeric Entry: asks you to fill in a blank
Quant Comp questions usually revolve around algebra, arithmetic, and geometry. Make sure you understand all of the major attributes and formulas associated with shapes, particularly circles and triangles. Shapes are not drawn to scale on the GRE, so never try to estimate lengths, angles, or areas based on what you see.
Many types of questions are multiple choice. Coordinate systems are drawn to scale and will usually require knowledge of what a slope is and how to solve for it. Sometimes you’ll be given coordinates directly, and other times you’ll need to use the coordinate system to look for points yourself. For probability problems, some may offer answer choices written using decimal points instead of as fractions, so familiarize yourself with what decimal points equal what fractions (e.g., $3/4=0.75$, $1/5=0.2$, etc.).
Numeric-entry questions can be answered using either numbers (with decimal points) or fractions. If a numeric-entry question asks for a fraction, chances are it’s either a probability or a percent (as a fraction) question. Note that you do not have to reduce a fraction. For example, you can type $20/80$ and it’ll be correct; you don’t have to reduce it to $1/4$.
Last, be aware data sets usually have multiple questions regarding the data. Graphs, like coordinate systems, are drawn to scale, and you’ll often come across questions concerning percentages and statistics. So make sure you know how to calculate averages, percentages, and percent changes. And definitely know your terminology (e.g., mean, mode, median, etc.)!

#3: Understand the Underlying Math Concepts
While memorization is a reliable method for getting these GRE math formulas under your belt, you should also try to actively understand the concepts behind them. Knowing what these formulas signify and how they’re connected to other formulas is particularly helpful for those struggling to memorize all of them.
What do I mean by this exactly? Let’s look at a couple of examples.
First off, it’s important to know the definitions of the vocab words used in these formulas. Let’s say a question requires you to solve for the perimeter of a rectangle. Even if you can’t recall the perimeter formula (which is $P=2l+2w$), start by asking yourself whether you know what a perimeter is or not. Hopefully, you remember a perimeter is the total length around a shape, or the total length of all sides of a shape. In other words, just add up the four sides of a rectangle! By knowing just the definition of the term, you can solve for the perimeter of a rectangle, with or without a formula.
But remembering a definition isn’t always enough. Sometimes, you have to look for relationships among formulas in order to understand why they are the way they are.
Here’s an example. Look at the area formula for a triangle and compare it to the area formula for a rectangle. For the rectangle, another way of writing the area formula is b (which is the same as the length) multiplied by h (which is the same as the width). The two formulas look like this:
Triangle: $A={1/2}bh$
Rectangle: $A=bh$
Starting to notice any similarities? Let’s keep going. Our rectangle has a base of 5 and a height of 2. Our triangle also has a base of 5 and a height of 2. According to our formulas, then, the area of the rectangle is 10, and the area of the triangle is 5. Here’s what our two shapes look like overlaying each other:
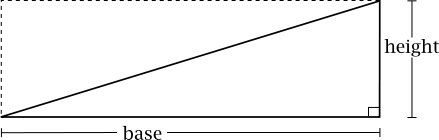
Can you see now why the area formula of a triangle is half the area formula of a rectangle? If we were to multiply our triangle’s base by its height without dividing by 2, we’d get the area of our rectangle — which is, as we can see, double the size of the triangle. Thus, knowing this relationship can help you solve a question on the GRE, even if you’re struggling to recall the triangle area formula.
Of course, not all GRE math formulas are as overtly connected as these two formulas are. Unfortunately, most of the time all you can really do is memorize a formula as is. For example, formulas like the Pythagorean theorem are those “you-get-what-you-see” types of formulas. Don’t bother spending any time trying to understand how Pythagoras actually came up with the formula — just memorize the more complicated ones and move on.

Is This All You Need for GRE Math?
In a word, no. Although these formulas are helpful and often necessary for doing well on the GRE, familiarizing yourself with this list alone doesn’t guarantee you an excellent Quant score.
To perform well on Quant, you must know, in addition to formulas, how to interpret data correctly, how to understand what a question is asking you to solve, and what basic terms like “quotient” and “prime number” mean. You should also know how to factor polynomials and how to compare quantities using ratios. These are just a handful of the several areas of math you’ll be tested on. To learn more about what exactly you should know for Quant, check out our in-depth math review.
As a final word of advice, always remember to use PEMDAS (the order of operations), consult your calculator when necessary, and, above all, practice, practice, practice! Good luck!
What’s Next?
Ready to put these formulas to the test? Search confidently for reliable Quant resources and practice questions using our GRE math practice guide.
Curious about what a good Quant score is? Check out our expert guide to setting a GRE math score goal.
Looking for test-day strategies? Check out our guide on how to use the GRE calculator, and don’t forget to take a look at our article on the most productive ways you can use your GRE scratch paper.
Ready to improve your GRE score by 7 points?
We've written a eBook about the top 5 strategies you must be using to have a shot at improving your GRE score.
Download it for free now:

