So, you were trying to be a good test taker and practice for the GRE with PowerPrep online. Buuuut then you had some questions about the quant section—specifically question 4 of Section 6 of Practice Test 1. Those questions testing our knowledge of Real Numbers can be kind of tricky, but never fear, PrepScholar has got your back!

Survey the Question

Let’s search the problem for clues as to what it will be testing, as this will help shift our minds to think about what type of math knowledge we’ll use to solve this question. Pay attention to any words that sound math-specific and anything special about what the numbers look like, and mark them on our paper.

The question references a number line, so it likely tests our Real Numbers math skill. Let’s keep what we’ve learned about this skill at the tip of our minds as we approach this question.

What Do We Know?

Let’s carefully read through the question and make a list of the things that we know.

 

1. The distance between $x$ and $0$ is $3$
2. We want to compare the distance between $x$ and $2$ to the value $2$

 

Develop a Plan

We know that the distance between $x$ and $0$ is $3$. The key to this question is realizing that $x$ could be $3$ units greater than $0$ or $3$ units less than $0$. So if $x$ is $3$ units greater than $0$, then $x=0+3=3$. Or if $x$ is $3$ units less than $0$, then $x=0-3=-3$. Let’s draw a number line on our paper, label $0$ on it, and also label the two values of $x$ we just found.

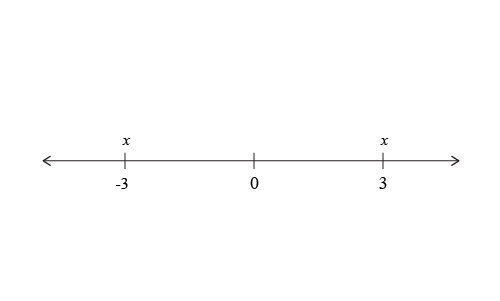
Since we want to know the distance between $x$ and $2$, let’s label $2$ on our figure and calculate how far away $x$ and $2$ are.

Solve the Question

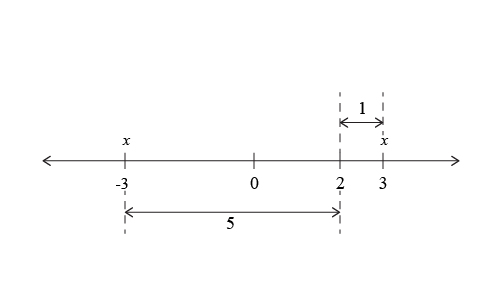
Here we can see that when $x=3$, then the distance between $3$ and $2$ is $3-2=1$. When $x=-3$, the distance between $-3$ and $2$ is $2-(-3)=2+3=5$. So Quantity A is either $1$, which is less than Quantity B, or $5$, which is greater than Quantity B. Since we found scenarios where Quantity A is less than Quantity B and also where Quantity A is greater than Quantity B,
the correct answer is D, the relationship cannot be determined from the information given.

What Did We Learn

Drawing the number line on our paper really helped to simplify this question. Let’s always feel free to make our own figures whenever the question omits a figure and we think that it could help us.

Also, let’s keep in mind that even though we have two different values for $x$, that does NOT imply that we don’t have enough information to solve this question. We still need to test the two different values for $x$.

 

Want more expert GRE prep? Sign up for the five-day free trial of our PrepScholar GRE Online Prep Program to access your personalized study plan with 90 interactive lessons and over 1600 GRE questions.

Have questions? Leave a comment or send us an email at [email protected].