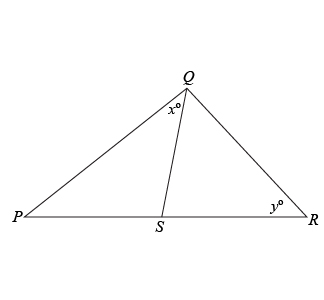
$$PS=SR$$
| Quantity A | $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ | Quantity B |
| $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ | ||
| $x$ | $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ | $y$ |
- Quantity A is greater.
- Quantity B is greater.
- The two quantities are equal.
- The relationship cannot be determined from the information given
So, you were trying to be a good test taker and practice for the GRE with PowerPrep online. Buuuut then you had some questions about the quant section—specifically question 4 of Section 4 of Practice Test 1. Those Triangle questions can be kind of tricky, but never fear, PrepScholar has got your back!
Survey the Question
Let’s search the problem for clues as to what it will be testing, as this will help shift our minds to think about what type of math knowledge we’ll use to solve this question. Pay attention to any words that sound math-specific and anything special about what the numbers look like, and mark them on your paper.
Hmm…since the problem has a triangle drawn and is asking about the angles in that triangle, it probably tests our Triangles math skill from geometry.
What Do We Know?
Let’s carefully read through the question and make a list of the things that we know.
- We have two triangles
- They share one side
- Two of their other sides are equal in length
- We want to compare two angles between the triangles
Develop a Plan
Since this is a Quantitative Comparison question, we don’t need to know the values of angles $x$ and $y$ in Quantities A and B. We just need to determine if one of the angles is bigger than the other. Since we are not specifically told that the figure is drawn to scale, we cannot assume that the figure is drawn to scale. For Quantitative Comparison questions, it is often times helpful to think of the extreme values the quantities can have so that we can determine the range of possible values for each quantity. So let’s try to redraw the triangles in ways that can capture the extreme possible values for angles $x$ and $y$.
Solve the Question
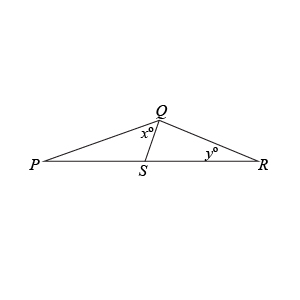
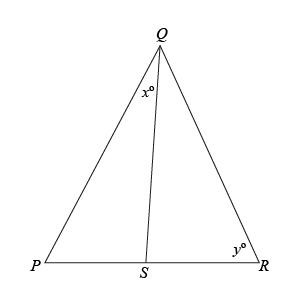
We know that sides $PS$ and $SR$ must be equal. However, the triangle doesn’t have much else in terms of things to constrain it. Let’s arbitrarily choose one of the quantities and try to find its extreme values. Quantity B is angle $y$, so let’s try to draw triangles with $y$ as small as possible and $y$ as large as possible to capture its range of extreme values.
We know that as the side opposite of an angle within a triangle increases, that angle also increases. So, if we want to vary angle $y$, then let’s change the length of the side of the triangle that is opposite of angle $y$, which is side $QS$.
Drawing a triangle with a short length for $QS$ we get:
What Did We Learn
When we are not explicitly told that a figure is drawn to scale, we CANNOT ASSUME that it is drawn to scale. In fact, the most effective solution method might be finding ways to change the figure without violating any information given in the problem. This is particularly useful for Quantitative Comparison questions with figures where we are NOT specifically told that they are drawn to scale.
We also learned that a great way to vary the angle within a triangle is to change the length of the side opposite that angle.
Want more expert GRE prep? Sign up for the five-day free trial of our PrepScholar GRE Online Prep Program to access your personalized study plan with 90 interactive lessons and over 1600 GRE questions.
Have questions? Leave a comment or send us an email at [email protected].