 The ratio of the number of male freshmen to the number of female sophomores is approximately
The ratio of the number of male freshmen to the number of female sophomores is approximately
- $2$ to $1$
- $3$ to $1$
- $3$ to $2$
- $4$ to $1$
- $5$ to $3$
So, you were trying to be a good test taker and practice for the GRE with PowerPrep online. Buuuut then you had some questions about the quant section—specifically question 14 of Section 6 of Practice Test 1. Those questions testing our knowledge of Graphical Methods for Describing Data can be kind of tricky, but never fear, PrepScholar has got your back!
Survey the Question
Let’s search the problem for clues as to what it will be testing, as this will help shift our minds to think about what type of math knowledge we’ll use to solve this question. Pay attention to any words that sound math-specific and anything special about what the numbers look like, and mark them on our paper.
Looks like we’ll need to analyze two tables containing data in this question, so it likely will draw on what we’ve learned about Graphical Methods for Describing Data. Let’s keep what we’ve learned about this skill at the tip of our minds as we approach this question.
What Do We Know?
Let’s carefully read through the question and make a list of the things that we know.
- We want to find the ratio of male freshmen to female sophomores
Develop a Plan
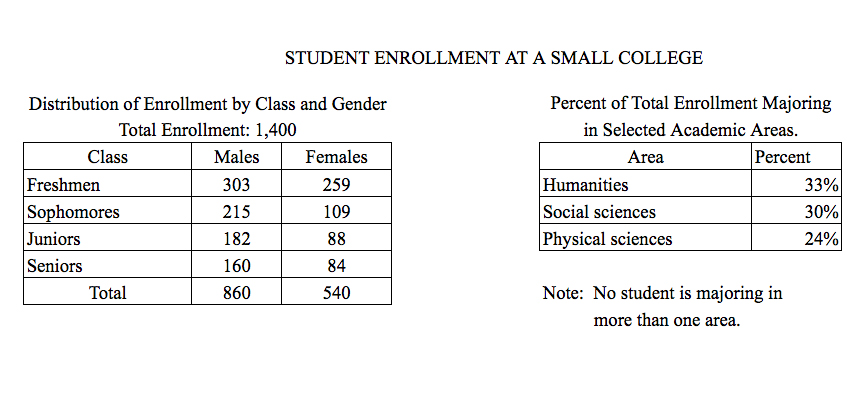
Let’s quickly scan the two tables to see what they have. The first table seems to be a two-way table for the class of a student (Freshmen, Sophomores, Juniors, or Seniors) and the gender of a student (Male or Female). The second table appears to show the percent of all students in three different majors.
The question asks for the ratio of male freshmen to female sophomores. In two-way tables, we often need to figure out if we’re being asked about an intersection between a column and a row or a union between a column and a row. Let’s remember that intersections are where a column and a row cross, so it’s where the row AND the column coexist. Unions are where the row OR the column exist.
Implied in the phrase “male freshmen” is that a student is male AND that the student is in the freshmen class. Therefore, we want to look for the intersection of the male column with the freshmen row. The value where the two cross each other is $303$.
Similarly, “female sophomores” implies that a student is a female AND in the sophomore class. The female column and sophomore row have the value $109$ at their intersection.
Now let’s see which answer choice gives the best estimate for the ratio between the number of male freshmen and the number of female sophomores.
Solve the Question
We want the ratio of male freshmen to females sophomores:
$$\Male \Freshmen \to \Female \Sophomores$$
Let’s plug in the two values we just found for these quantities.
$$303 \to 109$$
The answer choices all have single digits in their ratios (e.g. $2$ to $1$). Looking at our numbers, it appears that $303 \to 109$ is very close to $300 \to 100$, which would simplify to $3 \to 1$. While we could use our calculator to find the exact ratio, found when we divide $303$ by $109$, the question is designed to reward us for being able to estimate the ratio. Estimation here will allow us to finish the question sooner, giving us more time to spend on hard questions or question topics that we might struggle with in this section. Unlike your sports team coach told us, we don’t need to put forth $110$ percent effort here. The goal is to do just enough work to answer the question, then move on to the next one.
The answer is B, $3 \to 1$.
What Did We Learn
Sometimes GRE math questions want to test our confidence in our math ability and our comfort level with numbers. Must we see the exact number for this ratio? Going down that path will force us to use the clunky GRE calculator. Or, are we comfortable with estimations? Sometimes being good at math is just being good at estimations. At a formal business lunch, it would be quite inappropriate to whip out a calculator over appetizers just to see the exact value of some numbers being discussed. Let’s learn this lesson now, and improve our confidence and comfort level with numerical estimations!
Want more expert GRE prep? Sign up for the five-day free trial of our PrepScholar GRE Online Prep Program to access your personalized study plan with 90 interactive lessons and over 1600 GRE questions.
Have questions? Leave a comment or send us an email at [email protected].

