| Quantity A | $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ | Quantity B |
| $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ | ||
| $x$ | $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ | $y$ |
- Quantity A is greater.
- Quantity B is greater.
- The two quantities are equal.
- The relationship cannot be determined from the information given.
So, you were trying to be a good test taker and practice for the GRE with PowerPrep online. Buuuut then you had some questions about the quant section—specifically question 1 of the second Quantitative section of Practice Test 1. Those questions testing our knowledge of Triangles can be kind of tricky, but never fear, PrepScholar has got your back!
Survey the Question
Let’s search the problem for clues as to what it will be testing, as this will help shift our minds to think about what type of math knowledge we’ll use to solve this question. Pay attention to any words that sound math-specific and anything special about what the numbers look like, and mark them on your paper.
We want to compare the lengths of two sides in different triangles, so naturally we will expect to use our Triangles math skill. Let’s keep what we’ve learned about this skill at the tip of our minds as we approach this question.
What Do We Know?
Let’s carefully read through the question and make a list of the things that we know.
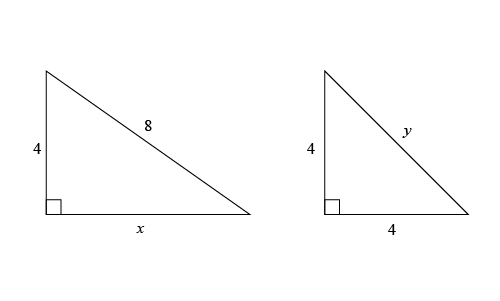
- We have a right triangle where we’re given the length of one leg and the hypotenuse, and we have an unknown length $x$ of the other leg
- We have a right triangle where we’re given the lengths of two legs and have an unknown length $y$
Develop a Plan
Let’s start with a top-down approach, where we will begin with what we’re looking for and work down to the details of what we’re given in this question. We want to compare $x$ with $y$. They’re both sides of right triangles where two of the side lengths in each triangle are given. We know that for right triangles we can use Pythagorean’s Theorem ($a^2+b^2=c^2$) to find out the length of a missing side, though we should be on the lookout for a quicker way to calculate these lengths, if we can find it. So let’s calculate sides $x$ and $y$ then compare their values.
Solve the Question
When we’re solving for the missing side of a right triangle, we should look out for Pythagorean Triples where the ratios of the two legs and the hypotenuse are ($3:4:5$) or ($5:12:13$). We should also look out for special right triangles where the sides have certain ratios based upon the angles in the triangle. If the angles are $30°, 60°, \and 90°$ then the sides OPPOSITE of those angles have lengths in the ratio of $(1, √3, \and 2)$, respectively. If the angles are $45°, 45°, \and 90°$ then the sides OPPOSITE of those angles have lengths in the ratio of $(1, 1, \and √2)$, respectively. If we come across a right triangle on the GRE, there’s a very good chance that the optimal solution will either utilize Pythagorean Triples or special right triangles based upon the angles $(30°:60°:90°\; \OR\; 45°:45°:90°)$.
Looking at the triangle with side $x$, we can see that $x$ is a side of a right triangle where the hypotenuse is double the length of one of the legs. We know that for a $(30°, 60°, 90°)$ right triangle, the hypotenuse is twice as long as the side that is opposite of the $30°$ angle, since the sides are in the ratio $(1, √3, \and 2)$. So this looks to be a ($30°, 60°, 90°$) right triangle. The side opposite the $60°$ angle is equal to the side opposite the $30°$ angle multiplied by $√3$, so $x = 4√3$.
Looking at the triangle with side $y$, we can see that $y$ is the hypotenuse and the two legs are equal. We know that for a $(45°, 45°, 90°)$ right triangle, the two legs are equal in length, so this is a $(45°, 45°, 90°)$ right triangle where the hypotenuse can be found by multiplying one of the legs by $√2$, so $y = 4√2$.
So now we have that Quantity A is $4√3$ and Quantity B is $4√2$. Both quantities have $4$ in them, but Quantity is multiplied by a bigger number $(√3>√2)$, so we know that Quantity B is greater than Quantity A.
The correct answer is A, Quantity A is greater.
What Did We Learn
For questions with triangles, we should be on the lookout for right triangles that have angles of $30°, 60°, \and 90°$ or $45°, 45°, \and 90°$. These are special cases where we know the ratios of the lengths of their sides. For a $30°, 60°, 90°$ triangle, the sides have the ratio $1, √3, \and 2$. For a $45, 45, 90$ triangle, the sides have the ratio $1, 1, \and √2$.
Want more expert GRE prep? Sign up for the five-day free trial of our PrepScholar GRE Online Prep Program to access your personalized study plan with 90 interactive lessons and over 1600 GRE questions.
Have questions? Leave a comment or send us an email at [email protected].

