USED CARS SOLD LAST MONTH AT CAR DEALERSHIP $X$
Indicate all such prices.
- $\$5{,}500$
- $\$6{,}500$
- $\$7{,}000$
- $\$8{,}500$
- $\$9{,}500$
- $\$10{,}500$
So, you were trying to be a good test taker and practice for the GRE with PowerPrep online. Buuuut then you had some questions about the quant section—specifically question 8 of the second Quantitative section of Practice Test 1. Those questions testing our knowledge of Graphical Methods for Describing Data can be kind of tricky, but never fear, PrepScholar has got your back!
Survey the Question
Let’s search the problem for clues as to what it will be testing, as this will help shift our minds to think about what type of math knowledge we’ll use to solve this question. Pay attention to any words that sound math-specific and anything special about what the numbers look like, and mark them on our paper.
The question gives us a table displaying numerical information, so we will likely draw upon what we’ve learned about Graphical Methods for Describing Data. Let’s keep what we’ve learned about this skill at the tip of our minds as we approach this question.
What Do We Know?
Let’s carefully read through the question and make a list of the things that we know.
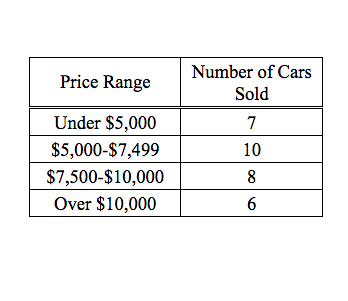
- We have a table containing price ranges and the number of cars sold in each price range
- A total of $31$ cars were sold
- We want to know which answer choices could possibly be the median price of the cars sold
Develop a Plan
We want to find which answer choices could be the median price of $31$ cars sold. The median of a list of numbers is the value right in the middle IF we place the values in order from least to greatest. So half of the values should be less than the median, and half should be greater than the median. If we divide $31$ by $2$, we get $15.5$. Hmm, we can’t have $15.5$ prices less than the median price. Ah! That extra half of a car must be the car with the median price, since it’ll be split between the lower half and upper half of the set of values. So we should use $15$ instead of $15.5$. That makes a bit more sense. Okay, so with $31$ different prices, we’ll have $15$ prices below the median, then the median price, and then $15$ prices above the median. So the median price would be the $16\t\h$ price if we were counting from the least price toward the greatest price. Let’s plan to use our table to find out which car is the $16\t
h$ if we count from the lowest price and up.
Solve the Question
From the table, we can see that, going from least to greatest in terms of car price, the first $7$ cars are under $\$5{,}000$.
Then the next $10$ prices are between $\$5{,}000$ and $\$7{,}499$. So we have the first $7$ cars, then cars $8$ through $17$ fall in the $\$5{,}000$ to $\$7{,}499$ price range. Ah ha! The $16\t\h$ car must be in the $\$5{,}000$ to $\$7{,}499$ price range!
Choosing any answers between $\$5{,}000$ and $\$7{,}499$, we find that the correct answers are A, B, and C.
What Did We Learn
Well, this was an interesting way to test our knowledge about medians. Looks like a good way to find the position of the median term is to just divide the number of values by $2$. We’ll just need to keep in mind that if we have an odd number of values, then the median value will be split between the upper and lower halves of our set of values. But we can fix that by just subtracting $0.5$ from our result, just like how we found that if we have $31$ cars, then $31/2-0.5$, or $15$ cars will be below the median price.
Want more expert GRE prep? Sign up for the five-day free trial of our PrepScholar GRE Online Prep Program to access your personalized study plan with 90 interactive lessons and over 1600 GRE questions.
Have questions? Leave a comment or send us an email at [email protected].

