So, you were trying to be a good test taker and practice for the GRE with PowerPrep online. Buuuut then you had some questions about the quant section—specifically question 14 of the second Quantitative section of Practice Test 1. Those questions testing our knowledge of Graphical Methods for Describing Data can be kind of tricky, but never fear, PrepScholar has got your back!

Survey the Question

Let’s search the problem for clues as to what it will be testing, as this will help shift our minds to think about what type of math knowledge we’ll use to solve this question. Pay attention to any words that sound math-specific and anything special about what the numbers look like, and mark them on our paper.

Looks like we’ll need to analyze two tables containing data in this question, so it likely will draw on what we’ve learned about Graphical Methods for Describing Data. Let’s keep what we’ve learned about this skill at the tip of our minds as we approach this question.

What Do We Know?

Let’s carefully read through the question and make a list of the things that we know.

 

1. We want to find the percent of the females who are juniors

 

Develop a Plan

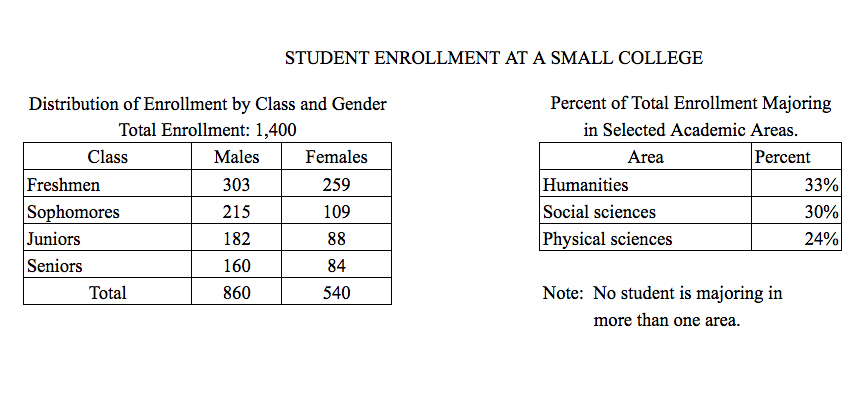
Let’s quickly scan the two tables to see what they have. The first table seems to be a two-way table for the class of a student (Freshmen, Sophomores, Juniors, or Seniors) and the gender of a student (Male or Female). The second table appears to show the percent of all students in three different majors.

The question asks, “Approximately what percent of the females are juniors?” Let’s break down this question into parts, to make sure we understand it completely.

“Approximately what percent of the females are juniors?”

The first part tells us we’re calculating a percentage. We know that a percentage worded this way in a two-way table will be the percentage equivalence of a proportion. In other words, we want to calculate:

$$\Percentage={\Successes}/{\Total}·100%$$

Let’s read the rest of the question to determine what values to put in for “Successes” and “Total.”

“Approximately what percent of the females are juniors?”

This is extremely important here. This “of” statement is called a conditional probability. It tells us that we ONLY want to look at the female students. In other words, the females make up the “Total” since we don’t want to even consider the males. We might even want to put our finger over the Male column to make sure that we don’t look at those numbers when answering this question.

The column total under “Female” is $540$, so for this question $\Total=540$. Let’s continue with the last part of the question.

“Approximately what percent of the females are juniors?”

Here we see that we only want to count successes if someone is a junior. Keep in mind, however, that we already crossed off the Male column, so here we will only count successes as the number of females who are juniors. Looking at our table where the Female column intersects the Junior row, we have $\Successes=88$. We now have enough information to calculate our percentage!

Solve the Question

Using our percentage equation, with $\Successes = 88$ and $\Total =540$, we get:

$$\Percentage=88/540·100%=16.3%$$

So the right answer is A, $16%$.

What Did We Learn

Probability questions and two-way tables! Here we had to be very careful about what numbers we chose. Breaking down the question into three separate parts was definitely a very helpful way to pinpoint exactly which numbers we should use in our calculation. Let’s keep in mind that for conditional probabilities, we’ll want to cross off part of our table to make sure we only pay attention to the part we’re interested in.

 

Want more expert GRE prep? Sign up for the five-day free trial of our PrepScholar GRE Online Prep Program to access your personalized study plan with 90 interactive lessons and over 1600 GRE questions.

Have questions? Leave a comment or send us an email at [email protected].