
Geometry might not be your strong suit, but you’re going to encounter it on GRE Quant, guaranteed. So how can you score highly on it? What are the formulas, rules, and terms you’ll need to know so you can solve GRE geometry problems quickly and accurately?
In this extensive GRE geometry review, we’ll go over the basics of geometry, including the major rules and formulas, and offer detailed explanations for official practice questions. We’ll also cover techniques for studying geometry as well as how you can effectively approach these questions on test day.
GRE Geometry Overview
Geometry is one of four major math subjects tested on the GRE, in addition to arithmetic, algebra, and data analysis. ETS (the company that proctors the GRE) doesn’t specify how many geometry problems are on the test, but we estimate roughly 15 percent of Quant centers on geometry, with triangles being one of the most commonly tested shapes. Clearly, geometry plays a pretty big role on the GRE!
But what exactly is geometry? If you’re envisioning shapes, you’re mostly correct. The bulk of GRE geometry revolves around circles and polygons (closed 2-D shapes created using straight lines), such as triangles, rectangles, and squares. You’re also very likely to encounter angles, lines, and inscribed shapes (shapes within shapes).
On the GRE, geometry problems come in a variety of forms. You may encounter them as multiple-choice questions, Numeric Entry questions, or Quantitative Comparisons. Some may provide you with diagrams (not drawn to scale!) or a combination of numbers and letters.
With all of these different forms, how can you learn to recognize a geometry problem on the GRE? And how will you know how to solve it? First, let’s take a look at some of the basic rules and formulas.
Quick side note: we've created the world's leading online GRE prep program that adapts to you and your strengths and weaknesses. Not sure what to study? Confused by how to improve your score? We give you minute by minute guide.
You don't NEED a prep program to get a great GRE score. But we believe PrepScholar is the best GRE prep program available right now, especially if you find it hard to organize your study schedule and don't know what to study.
Click here to learn how you can improve your GRE score by 7 points, guaranteed.
61 GRE Geometry Formulas and Rules You Must Know
You can’t study GRE geometry without knowing what to study. Here is a list of the major rules and formulas you should have down by test day.
#1: Rules of Angles
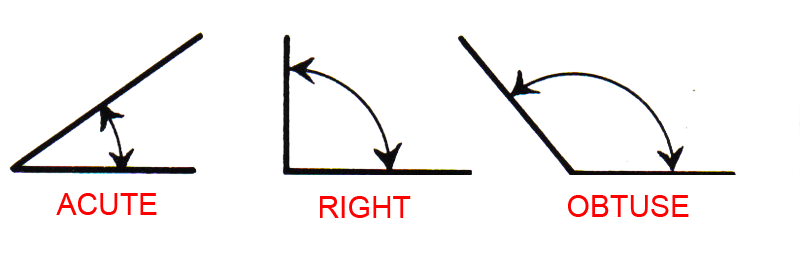
- A straight line is equal to 180 degrees.
- An acute angle is any angle less than 90 degrees.
- An obtuse angle is any angle between 90 and 180 degrees.
- A right angle is equal to 90 degrees and is usually signified by a small square:
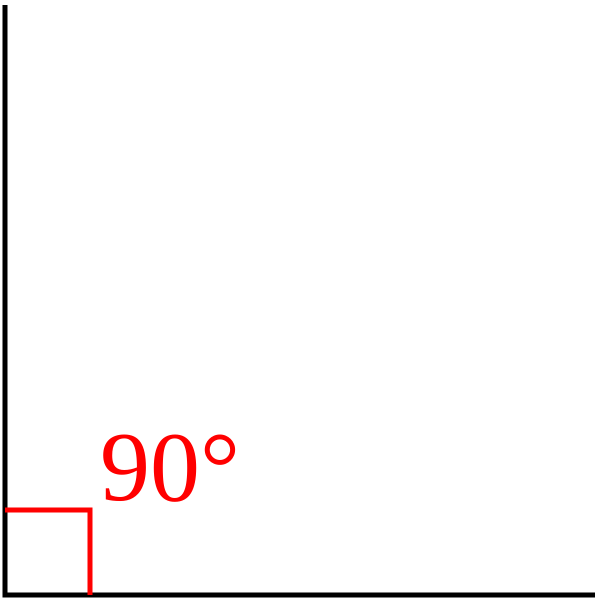
- The symbol ∠ is often used to denote an angle. For example: angle A=∠A.
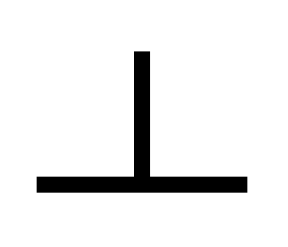
- Two lines that intersect to create 90-degree angles are perpendicular to each other:
- Two lines that never intersect and have the same slope are parallel to each other:

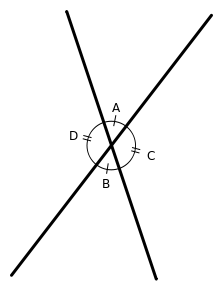
- When two lines intersect, four angles are created:
- opposite angles are equal in measure ($∠A=∠B$, $∠C=∠D$).
- adjacent angles add up to 180 degrees ($∠A+∠D=180$, $∠A+∠C=180$, $∠B+∠D=180$, $∠B+∠C=180$).
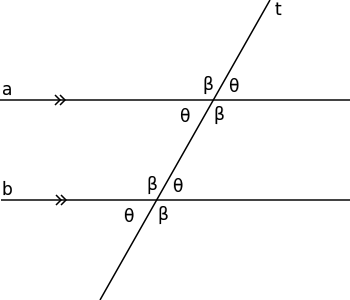
- When a line intersects two parallel lines, eight angles are created:
- corresponding angles are equal in measure.
- alternate interior angles are equal in measure.
- alternate exterior angles are equal in measure.
- consecutive interior angles add up to 180 degrees.
#2: Squares

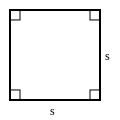
Rules
- All sides are equal in length.
- Opposite sides are parallel to each other.
- All interior angles are right angles.
- The perimeter is the total length of all sides.
Formulas
Perimeter
$P=4s$
- s = side
Area
$A=s^2$
#3: Rectangles

Rules
- Opposite sides are equal in length and parallel to each other.
- All interior angles are right angles.
- The perimeter is the total length of all sides.
Formulas
Perimeter
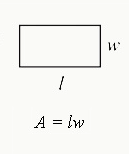
$P=2l+2w$
or
$P=2b+2h$
- l = length, w = width
- b = base (same as length), h = height (same as width)
Area
$A=lw$
or
$A=bh$

For this Numeric Entry question, we must figure out the perimeters for rectangle R and square S. All we have to do is use the perimeter formulas (as described above) for rectangles and squares.
R has a length of 30 and a width of 10, so let’s plug in these numbers to our perimeter formula for rectangles:
$2(30)+2(10)=80$
This gives us a perimeter of 80 for R. Now, let’s solve for the perimeter of S. Because S is a square, all we have to do is multiply the length of one of its sides by 4 to get its perimeter. Using the perimeter equation for squares, we get:
$4(5)=20$
Now, we’re left with a perimeter of 80 for R and a perimeter of 20 for S. But what do we do with these numbers? The question is asking what fraction perimeter S is of perimeter R. In other words, we need to set up a ratio comparing perimeter S to perimeter R.
Want to improve your GRE score by 7 points? We have the industry's leading GRE prep program. Built by world-class instructors with 99th percentile GRE scores, the program learns your strengths and weaknesses through machine learning data science, then customizes your prep program to you so you get the most effective prep possible.
Try our 5-day full access trial for free:
If perimeter S is 20 and perimeter R is 80, our fraction is $20/80$. You can write $20/80$ in the blank (with 20 as the numerator and 80 as the denominator), or reduce the fraction to $1/4$. The GRE doesn’t require you to reduce fractions, so any equivalent fraction (e.g., $2/8$, $5/20$, etc.) is correct.
#4: Circles

Rules
- A circle is equal to 360 degrees.
- The circumference is the length around a circle (i.e., the perimeter of a circle).
- The radius (plural: radii) is the length from the middle of a circle to any point on the edge of a circle.
- The diameter is the length of any straight line cutting a circle in half (and passing through the center point).
- The radius is half the length of the diameter (and the diameter is twice the length of the radius). So, $2r=d$.
- π (pi) can be rounded to 3.14.
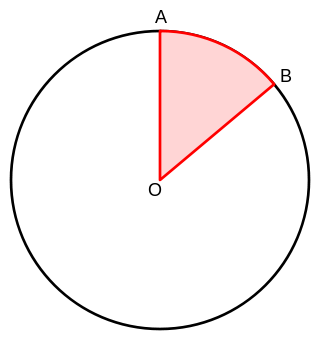
- An arc is all points between two points on the edge of a circle (AB).
- A sector is the (shaded) region enclosed by an arc and two radii (AOB).
- A central angle is the angle created by the intersection of two radii at the center of a circle (∠O).
Formulas
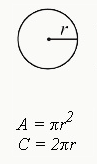
Circumference
$C=2πr$
or
$C=πd$
- r = radius, d = diameter
Area
$A=πr^2$
Length of an Arc
$$\arc \length=2πr{\central \angle \of \arc}/360$$
Area of a Sector
$$\area \of \sector=πr^2{\central \angle \of \sector}/360$$
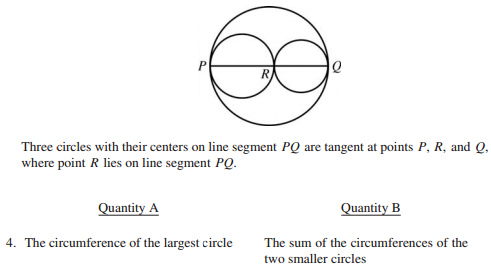

Here, we’re being asked to compare the circumference of the large circle (we’ll call it circle A) with the sum of the circumferences of the two smaller circles (we’ll call them circles B and C). What we need for this problem is the circumference formula, or $C=2πr$.
However, we have no clue what the radius or diameter of circle A is, let alone the diameters or radii of circles B and C. As a result, you might be tempted to guess D. But let’s test out a couple of numbers first to see if they can reveal anything to us about the relationships between circles A, B, and C.
According to the diagram, circle A has a diameter of PQ (we don’t know what the center point is, so there’s no point using the radius for this problem). Therefore, we must use the diameter form of the circumference formula ($C=πd$).
Now, plug-in time. Let’s say circle A has a diameter of 10. Its circumference, then, would be:
$C=10π$
Because circles B and C make up the entire length of circle A‘s diameter, we know the sum of their diameters must equal circle A’s diameter (which is 10, in our case).
If circle B has a diameter of 6, its circumference would be 6π. Thus, circle C must have a diameter of 4 and a circumference of 4π. If we add these two circumferences together, we get 10π, which is the same as the circumference of circle A.
No matter what pair of numbers we choose for the diameters of circles B and C, whether it’s 5 and 5, 2 and 8, or 3 and 7, the two circumferences will always, when combined, equal 10π.
Therefore, the correct answer is C: The two quantities are equal.
#5: Triangles

Rules
- All interior angles add up to 180 degrees.
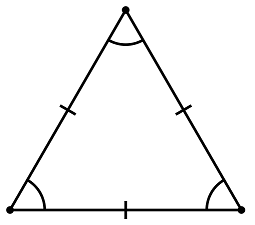
- There are three types of special triangles:
- equilateral: all sides are equal in length, and all interior angles are 60 degrees.
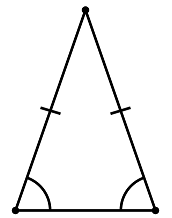
- isosceles: two sides are equal in length, and the two angles opposite the two equal sides are equal in measure.
- right: a triangle with one right angle. The longest side (opposite the right angle) is the “hypotenuse,” and the two shorter sides are the “legs.”
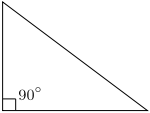
Formulas
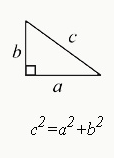
Pythagorean Theorem
$a^2+b^2=c^2$
- a = leg, b = leg, c = hypotenuse
- This theorem can only be used for right triangles.
- Certain triangle-side combinations (a:b:c) can be memorized. These are called Pythagorean triples. Common ones include:
- 3:4:5
- 5:12:13
- 8:15:17
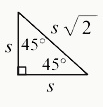
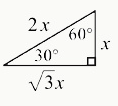
- There are also special right triangles:
- 45-45-90 triangle (isosceles right triangle): a triangle with one right angle and two 45-degree angles. Both legs are equal in length, and the ratio of its sides is x:x:√2x.
- 30-60-90 right triangle: interior angles are 30, 60, and 90 degrees. This type of triangle is equal to half of an equilateral triangle, and the ratio of its sides is x:√3x: 2x.
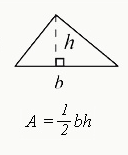
Want to improve your GRE score by 7+ points?
Check out our best-in-class online GRE prep program. We guarantee your money back if you don't improve your GRE score by 7 points or more.
PrepScholar GRE is entirely online, and it customizes your prep program to your strengths and weaknesses. We also feature 2,000 practice questions, official practice tests, 150 hours of interactive lessons, and 1-on-1 scoring and feedback on your AWA essays.
Check out our 5-day free trial now:
Area
$$A={1/2}bh$$
- b = base, h = height

You can try to figure out the problem just by looking at it, but it’s better to take a few seconds to draw a triangle. A right triangle with measures A, B, and C, and legs of lengths 4 and x, looks something like this:
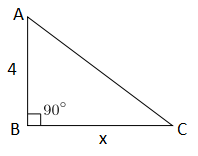
This triangle should stand out to you right away because it’s a right triangle with a leg of 4. Remember our Pythagorean triples? One of those is 3:4:5. If x equals 3 (answer choice C), then the hypotenuse must be 5 — which is more than 4 and less than 8. Immediately, we know C is a correct answer choice.
For the other answer choices, however, we’ll have to plug in each of the possible values of x and solve for the hypotenuse using the Pythagorean theorem ($a^2+b^2=c^2$). To avoid confusion (our angles are also called A, B, and C), let’s call the hypotenuse h. As long as the hypotenuse comes out to any number between 4 and 8, that answer choice is correct.
Start by solving for answer choice A, or 1:
$4^2+{1}^2=h^2$
$16+1=h^2$
$17=h^2$
$h=√{17}=4.12$
Answer choice A produces a hypotenuse slightly longer than 4, so this answer is correct, too. As 3 (answer choice C) produces a hypotenuse of 5, 2 must therefore produce a hypotenuse between 4.12 and 5 and can be marked correct, as well.
So far, we know answer choices A, B, and C are correct. Now, let’s solve for answer choice F, or 6. If the hypotenuse comes out to something below 8, we know answer choices D and E will also be between 4 and 8.
Here’s how to solve for h if x=6:
$4^2+{6}^2=h^2$
$16+36=h^2$
$52=h^2$
$h=√{52}=7.21$
Because answer choice F results in a hypotenuse less than 8, and answer choice A produces a hypotenuse more than 4, the correct answer choices are all of them: A, B, C, D, E, and F.

All we’re being asked to do here is take whatever info the question is giving us, plug it in to the area formula for a triangle, and simplify. That’s it!
In this question, we have a triangle with a base b and height h. This is just like the area formula, right? The only extra information we’re given is that b is twice the length of h, so $b=2h$.
Now, we just replace b with 2h in the area formula and simplify to get our answer:
$A={1/2}bh$
$A={1/2}(2h)h$
$A={h}(h)$
$A=h^2$
The correct answer is C: $h^2$.
#6: Trapezoids
Rules
- Opposite bases are parallel to each other.
Formulas
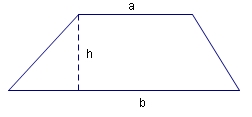
Area
$$A={1/2}(a+b)h$$
- a = $\base_1$, b = $\base_2$, h = height
#7: Parallelograms

Rules
- Opposite sides are equal in length and parallel to each other.
- Opposite angles are equal.
Formulas
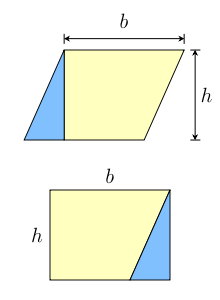
Area
$A=bh$
- b = base, h = height
#8: Rectangular Solids

Rules
- Rectangular solids are 3-D objects with six faces.
- Cubes are a type of rectangular solid with six equal faces (i.e., six squares) that are equal in length on all sides and equal in area.
- The volume is the amount of space a 3-D object occupies.
- The surface area is the total area of all sides of a 3-D object.
Formulas
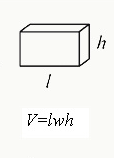
Volume
$V=lwh$
- l = length, w = width, h = height
Surface Area
$SA=2(lw+lh+wh)$
#9: Right Circular Cylinders

Rules
- Circular cylinders contain two congruent (identical) circular bases.
- The axis (the line running through the center of a cylinder) is perpendicular to the centers of its bases.
Formulas
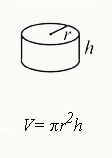
Volume
$V=πr^2{h}$
- r = radius (of circular face), h = height
Surface Area
$SA=2{πr^2}+2πrh$


If you’re not sure where to start, consider first the info this question is giving us: the radius and the volume of a right circular cylinder. Quantity A is asking for the height of the cylinder. So what formula could we use to solve this problem? More specifically, what formula contains the radius, height, and volume of a right circular cylinder?
That’s right — the volume formula for right circular cylinders. In other words, we need to plug in all of the info we’ve been given and solve for the height of the cylinder.
According to the question, the cylinder has a radius of 2 and a volume of 15. Let’s start by plugging in these numbers to our volume equation and simplifying:
$V=πr^2{h}$
$15=π({2})^2{h}$
$15=4π{h}$
Now, we just need to solve for h by dividing both sides by 4π. Remember, π can be rounded to 3.14, so 4π is approximately equivalent to 12.56. Divide 15 by 12.56 to get 1.19, which is clearly smaller than 2 inches. The correct answer is B: Quantity B is greater.

Resources and Tips for Your GRE Geometry Review
Geometry can be tricky to get right. Here are some tips for making your GRE geometry practice as helpful as possible.
#1: Memorize Key Concepts
Studying any math concept can be overwhelming at first, especially if you haven’t taken a math course in a while. But familiarizing yourself with some of the major geometry concepts should increase your confidence and ultimately help you perform well on any GRE geometry question that comes your way.
What are these key concepts? Here’s what you should strive to be an expert on before sitting for the GRE:
- Relationships between angles: Know exactly what an angle is, how it’s formed, and how it relates to other angles in a shape or when created by intersections of lines. Recognize any special properties associated with right angles. Additionally, remember that interior angles of triangles always add up to 180 degrees, a line equals 180 degrees, and a circle equals 360 degrees.
- Perimeter, area, and circumference: Have a clear understanding of the definitions of these terms and memorize their respective formulas for squares, rectangles, circles, and triangles. Although 3-D objects, trapezoids, and parallelograms are less commonly tested on the GRE, try to familiarize yourself with their rules and formulas, too.
- Pythagorean theorem: Memorize this theorem, as you’re extremely likely to use it at least once on the GRE.
- Special right triangles: Be able to recall the characteristics of special right triangles (45:45:90 and 30:60:90).
- π (pi): Don’t get confused if you see this symbol! Pi can be rounded to 3.14 to ease calculations.
- Definitions: Memorize the definitions of all basic geometry terms, such as radius, area, sector, etc. You can view a glossary of terms at the end of this article.

#2: Make Flashcards
One of the most effective ways to retain the key concepts of geometry (and other subjects) is to create flashcards. If you’re a fan of paper flashcards, write the formula, shape, or term on the front and its definition or explanation on the back. Always include diagrams or examples if possible so you have context for the concepts you’re learning.
You can also try making digital flashcards with a free downloadable software called Anki, which uses spaced-repetition software (SRS) to test you on difficult cards more often.
#3: Test Yourself With Realistic Practice Questions
To do well on Quant, and especially on GRE geometry problems, you must be aware of the exact types of questions you’ll encounter on test day. Realistic practice questions familiarize you with the types of geometry questions you’re likely to tackle on the GRE. And the more GRE geometry practice you do with GRE-like questions, the more quickly and accurately you should be able to answer such questions on test day.
Practice questions also expose you to the different ways geometry problems may be presented on the test. For example, not all geometry problems supply diagrams, and only occasionally do they tell you the exact formula you’ll need for solving a problem. So far, you’ve encountered a handful of sample practice questions in this article. All questions included here were taken directly from official ETS practice tests and are therefore extremely similar to the types of geometry questions on the actual GRE.
For additional practice questions, check out our articles on the best resources for math practice and where to find high-quality sample questions. You can also test your geometry knowledge using the free (and official) GRE practice tests listed in our guide.

How to Approach GRE Geometry on Test Day
If you’re new to the GRE, you’re probably wondering how you should approach geometry problems on test day so you don’t end up blanking or spending too much time on a single question. Let’s take a look at our best strategies for tackling GRE geometry questions effectively.
#1: Know What You Can and Cannot Assume
One technique you might’ve heard of is to estimate values using a given diagram. But this method is counterproductive because geometry diagrams on the GRE are not drawn to scale.
For example, look back at the sample question we covered in the section on circles. At a glance, you might assume point R is the center point of the largest circle; however, nowhere in the problem does it state this is the case. This lack of clarity in regard to the circle’s center point is how we ultimately know to focus on the diameter (which is clearly given to us as line PQ) instead of the radius.
Here are some other concepts and values you should refrain from assuming or visually estimating:
- Angles: If you’re not given sufficient info to be able to calculate a particular angle, don’t make any assumptions about its value (or even whether it’s acute or obtuse).
- Right angles: Don’t assume a shape contains a right angle unless it’s clearly denoted, either by a small square in the corner or in the wording of the problem itself. You can assume a shape has a right angle if it’s a natural quality of the shape. For example, if a problem describes a rectangular room (as the following practice question does), you can assume the room contains four right angles.
- Parallel lines: Never assume two lines are parallel unless specifically stated in the problem.
So what can you make assumptions about? Here are the areas of geometry that are perfectly OK to accept as they appear on the GRE:
- Any line appearing straight is assumed to be straight without any hidden bends or curves.
- Any shape appearing as a circle is a circle. Don’t expect to encounter ovals or other elliptical shapes.
- Any shape appearing as a polygon is a polygon. All 2-D shapes are closed shapes, with no gaps or overlapping lines (however, two shapes may overlap each other).
Lastly, all shapes and angles follow basic geometry rules. You won’t have to deal with any bizarre shapes or special geometry problems that don’t abide by the fundamental laws and formulas detailed above. Phew!

#2: Draw a Picture
Surprisingly, a lot of GRE geometry problems don’t supply you with diagrams, even when discussing key characteristics of shapes. The best way to tackle these problems, then, is to draw the shapes yourself.
By doing so, you’ll get a clearer idea as to what the question is asking you to do and be better able to understand how the given values correspond to one another. Drawing a picture can also help you determine what formula you’ll need to use to solve a particular problem.
Previously, I drew my own triangle for the sample question above using the Pythagorean theorem. Here’s another example of a question you could draw a diagram for:

For this question, the phrases “square feet” and “rectangular floor space” should give you a clear hint this problem has a huge geometry focus (specifically, area). Thus, it’ll be helpful to draw some diagrams.
Floor space is $15 per 30 square feet for one day. If Alice rented space measuring 8 by 15 feet, and Betty rented space measuring 15 by 20 feet, here are what their rooms would look like (not drawn to scale):
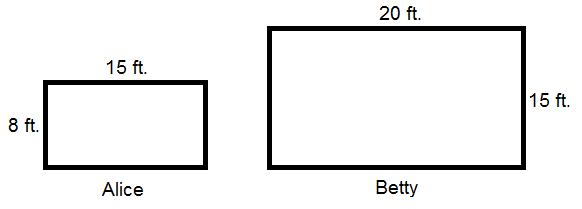
This diagram, with its lengths and widths, clarifies for us the problem has to do with area. We can then use the area formula for a rectangle ($A=lw$) to calculate the areas of each of their rooms:
Alice: $A=8(15)=120$
Betty: $A=15(20)=300$
Alice’s room is 120 square feet, whereas Betty’s is 300 square feet. If the cost of a room for one day is $15 per 30 square feet, all we have to do now is use cross multiplication to get the price of each of their rooms.
Alice: $15/30=x/120$
$1,800=30x$
$x=60$
Betty: $15/30=x/300$
$4,500=30x$
$x=150$
Although we didn’t need the diagram to solve the question, drawing out the rectangles for this problem helps us keep track of our values for Alice and Betty and clearly illustrates what formula we’ll be using with our given numbers (in this case, area).
According to our calculations, Betty paid \$150 and Alice paid \$60. If we subtract 60 from 150, we get a difference of 90. So, Betty paid $90 more than Alice. The correct answer is D: $90.

#3: Plug In Numbers
Certain questions, often Quantitative Comparisons, may give you geometry problems without offering any actual numbers or enough info to be able to plug in anything to a formula and solve it. Instead of assuming the answer is “D: The relationship cannot be determined from the information given,” try to first plug in made-up numbers to see what happens. This can also be done to verify a solution if you’ve already solved a problem using a different method.
If you look back at our previous sample question on circles, you’ll see we solved this equation by plugging in numbers and testing them out using the circumference formula. Here’s another example of how plugging in numbers can lend you a hand in solving a geometry problem:


For this question, we’re going to both draw a diagram and plug in some values. The two triangles being described are both equilateral triangles, meaning both triangles contain three sides with identical lengths. This is a huge deal, and we’ll explain why in a second.
Triangle T is 6 times bigger than triangle X because each of its sides is 6 times longer than each of the sides of X. Confused? Let’s say each side of X equals 1 and each side of T equals 6. Here’s what the two triangles would look like (not drawn to scale):
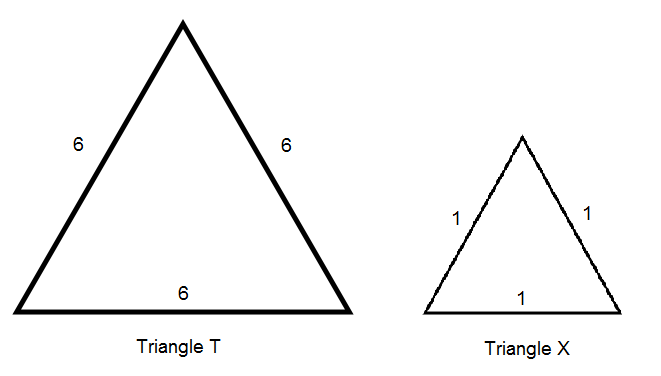
Now, all we need to do is take the ratios of any two sides of T and any two sides of X, and compare the ratios we get. Why can we do any two sides, you ask? Because both triangles are equilateral, it doesn’t matter which two sides we compare; all of an equilateral triangle’s sides are equal in length, so the ratio is the same for any two sides.
For T, the ratio of any two of its sides is 6:6, or, when reduced, 1:1. For X, the ratio of any two of its sides is also 1:1. Because these two ratios are the same, the correct answer is C: The two quantities are equal.
#4: Approach Inscribed Shapes as Two Separate Shapes
Some problems in your GRE geometry practice or on test day may give you diagrams with one shape inscribed in another (as you can see with the sample question on circles above). A polygon inscribed in a circle or a circle inscribed in a polygon are two common combinations you’ll see on the GRE. When a shape is inscribed in a circle, it means the inscribed shape’s vertices are tangent to the circle.
The easiest way to approach these problems is by first analyzing each shape independently. Always use a shape’s respective formula to solve for whatever the question is asking, such as area, circumference, etc.
If a problem asks you to solve for the area of a part of the larger shape where the inscribed shape is absent (e.g., the shaded region in the image below), what it’s really asking you to do is set up a subtraction problem. To solve this kind of problem, simply calculate the areas, separately, of both the main shape and the inscribed shape using their respective area formulas, and then subtract the inscribed shape’s area from the main shape’s area.

GRE Geometry: Glossary of Common Terms
The GRE expects you to have familiarity with the definitions of several terms related to shapes, angles, and formulas. To cap off our GRE geometry review, I offer you a glossary of common geometry terms. Memorize all of them and you’re sure to understand the majority of geometry questions you encounter! All terms are listed in alphabetical order.
- acute angle: any angle smaller than 90 degrees
- arc: all points between two points on the edge of a circle
- area: the amount of space enclosed by a 2-D shape
- axis: the line segment of a right circular cylinder that joins the center points of the circular bases; also refers to the horizontal (x-axis) and vertical (y-axis) reference lines in a coordinate system
- central angle: the vertex at the center of a circle created by the intersection of two radii
- circumference: the length around a circle (i.e., the perimeter of a circle)
- congruent: equal to or the same as in shape and size
- cube: a type of rectangular solid with six square faces that are all the same length and width (and share equal areas)
- diameter: the length of a straight line cutting a circle in half and passing through the center; equal to double the radius
- equilateral triangle: a triangle with three sides of the same length and three 60-degree angles
- isosceles triangle: a triangle with two sides of the same length and two equal angles
- obtuse angle: any angle larger than 90 degrees and smaller than 180 degrees
- parallel lines: lines that never intersect and have the same slope
- perimeter: the total length around a shape (i.e., the sum of all sides)
- perpendicular lines: lines that intersect to form right angles
- polygon: any 2-D shape created by straight lines, including triangles, squares, rectangles, parallelograms, and trapezoids
- quadrilateral: any four-sided polygon, such as squares, rectangles, parallelograms, and trapezoids
- radius (radii): the length of a straight line connecting the center of a circle to any point on the edge of the circle; equal to half the diameter
- rectangular solid: a 3-D object with six faces
- right angle: a 90-degree angle, usually designated by a small square
- right circular cylinder: a 3-D object with two congruent circular bases and an axis perpendicular to the centers of its bases
- right triangle: a triangle with a 90-degree angle, two legs (shorter sides), and a hypotenuse (the longest side)
- sector: any (shaded) region of a circle enclosed by an arc and two radii
- similar: two shapes with the exact same shape (and therefore the same angles) but different sizes; similar shapes share equal ratios of their sides and angles
- surface area: the total exterior area of a 3-D object
- tangent: a line or shape intersecting a shape at exactly one point
- vertex (vertices): the point at which two lines meet to form an angle
- volume: the space occupied by a 3-D object
What’s Next?
Looking to cover other Quant concepts besides geometry? Check out our exhaustive math review to learn more about what’s on the exam.
Geometry isn’t everything. Don’t forget to read our list of the most important formulas you’ll need for Quant.
Craving more math practice? Get tips and ideas on how to study for Quant using practice questions and tests. And for test-day strategies, read our guides on how to use your scratch paper and how to work the on-screen calculator.
Ready to improve your GRE score by 7 points?
We've written a eBook about the top 5 strategies you must be using to have a shot at improving your GRE score.
Download it for free now:


Comments are closed.