
Whether you’re a math major or one of those haven’t-studied-math-since-high-school types, the GRE is going to test you on a myriad of math topics, from shapes and symbols to tables and coordinate systems. And the only way you can attack the Quantitative Reasoning section head-on is by knowing exactly how the GRE plans to challenge you. In other words, what kind of math is on the GRE? What specific GRE math topics should you study ahead of time? And what do GRE math questions actually look like?
In this comprehensive GRE math review, we’ll explore the ins and outs of the GRE Quantitative Reasoning section, taking a look at the various concepts you’ll be tested on and providing you with our best tips for effective studying.
GRE Quantitative Reasoning Overview
The Quantitative Reasoning measure, also known as “Quant,” is one of three major components of the GRE. (The other two are Verbal Reasoning and Analytical Writing.)
You’ll always have two Quant and two Verbal sections, but the order in which you’ll complete them is entirely random. (You will also get a fifth experimental section that’ll be an additional Quant or Verbal section. This section is unscored, but there is no way to know which one is experimental, so always try your best on all of them!)
Quant is composed of 40 math questions. Each Quant section contains 20 questions and gives you 35 minutes. Although many, if not most, calculations can be performed mentally or on paper, you will have access to an on-screen calculator with basic arithmetic functions (including square roots).
If you are taking the paper version of the GRE (offered in countries where the computer version is unavailable), each Quant section contains 25 questions instead of 20, raising your grand total to 50 questions. You’ll also get an additional five minutes for each Quant section, and there is no experimental section (so you’ll always have exactly two Quant sections). A calculator will be provided to you upon arrival at the test center.
You’ll get ample scratch paper before the computer version of the GRE. This paper may be used for Quant, Verbal, AW, or any sections you choose (but is arguably most useful for writing calculations down during Quant).
Quick side note: we've created the world's leading online GRE prep program that adapts to you and your strengths and weaknesses. Not sure what to study? Confused by how to improve your score? We give you minute by minute guide.
You don't NEED a prep program to get a great GRE score. But we believe PrepScholar is the best GRE prep program available right now, especially if you find it hard to organize your study schedule and don't know what to study.
Click here to learn how you can improve your GRE score by 7 points, guaranteed.
Lastly, there’s the scoring system. Quant, like Verbal, is scored on a scale of 130-170. On this scale, 170 is a perfect score and 130 is the lowest possible score. At present, the average Quant score is 152.57.
What Kind of Math Is on the GRE?
So far, our GRE math review has covered the fundamentals of Quant. Now, let’s answer a slightly more challenging question: what kind of math is on the GRE?
Like the SAT and ACT, Quant deals with a breadth of mathematical concepts. Luckily, though, all GRE math topics are those you studied in middle school and high school. Even better? Quant doesn’t test any upper-level concepts like calculus and trigonometry. So go ahead and breathe a sigh of relief — Quant isn’t ridiculously difficult!
But what math is on the GRE? There are four major areas of math tested on Quant: arithmetic, algebra, geometry, and data analysis. Below, I introduce the definitions of these topics and explain the specific concepts most likely to appear on the GRE.

Arithmetic
Arithmetic is the basis of pretty much all math and is defined as the manipulation of numbers. On the test, arithmetic mostly deals with addition, subtraction, multiplication, and division, as well as:
- Integers, fractions, and decimals
- PEMDAS (order of operations)
- Exponents and square roots
- Absolute values
- Prime numbers
- Even and odd numbers
- Percents and percent changes
- Sequences
- Ratios, proportions, and cross multiplication
Algebra
Algebra is basically where numbers and letters (i.e., unknown numbers) come into play. GRE concepts include:
- Expressions and equations
- Variables and constants
- Inequalities
- Functions
- Coordinate systems
- Coordinate geometry
- Lines and slopes
- Factorization
Geometry
The bulk of geometry is the study of shapes and angles. More specifically, GRE geometry encompasses:
- Lines, parallel lines, and perpendicular lines
- Relationships among angles
- Types of angles
- Polygons, including triangles, rectangles, squares, trapezoids, and parallelograms
- Special right triangles and the Pythagorean theorem
- Circles
- Arcs and sectors
- 3-D objects, including rectangular solids and right circular cylinders
- Perimeter, area, circumference, volume, and surface area
- Similar shapes
- Inscribed shapes
Data Analysis
On the GRE, data analysis primarily focuses on your ability to interpret data by testing you on:
- Distribution of data and frequency
- Graphical representations of data, including bar graphs, pie charts, scatterplots, time plots, and histograms
- Statistics, including mean (average), median, mode, and range
- Quartiles and percentiles
- Standard deviation
- Factorials, permutations, and combinations
- Probability
- Bell curve and normal distribution

What Kinds of Questions Are on the GRE?
Content-wise, most GRE Quant questions are independent questions (also known as “discrete questions”) and are not directly related to any other question on the test. Non-discrete questions are the opposite and revolve around a single set of data, such as a table or graph.
There are four types of questions on Quant:
- Quantitative Comparison
- Multiple choice (one answer choice)
- Multiple choice (one or more answer choices)
- Numeric Entry
I’ll explain each of these question types in detail, showing you how they appear and function on the GRE.
Quantitative Comparison
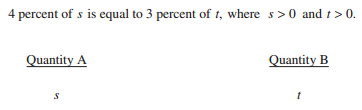
Often abbreviated to “Quant Comp,” Quantitative Comparison questions account for a little more than a third of Quant, with seven or eight questions per section. Quant Comp questions ask you to compare two quantities (Quantity A and Quantity B) and choose one of four possible answer choices:
- Quantity A is greater.
- Quantity B is greater.
- The two quantities are equal.
- The relationship cannot be determined from the information given.
These answer choices are always the same regardless of the content of the question.
GRE Quant Comp questions deal with all major math topics, with some focusing on algebraic expressions and equations, and others on integers, shapes, or percentages. Most Quant Comp questions supply you with a description, diagram, rule, or table, so you’ll have all of the relevant information you need to solve the problem.
Multiple Choice (Select One Answer Choice)

First off, there are two types of multiple-choice questions on GRE Quant: ones with a single correct answer, and ones with one or more correct answers. Here, we’ll discuss those with one correct answer.
Single-answer questions always offer five possible answer choices. Each choice is accompanied by an oval (or circle on the paper test) to show that you can only select one answer choice. ETS does not specify how many single-answer multiple-choice questions there are on the GRE, but we estimate they make up a little more than half of Quant. As a result, it’s important you familiarize yourself with how these questions function and what kinds of math they test.
For many single-answer questions, it’ll be better for you to solve the problem on your own and then compare the answer you come up with to the five possible answer choices (choosing the one identical to your result). Other times, however, it’ll be more convenient to just plug in the answer choices in order to find the correct answer.
Occasionally, a multiple-choice question will ask you to select an approximation. In this case, none of the answer choices will be an exact answer to the question. For example, the answer could be something like \$4,329.05, but the closest answer choice is \$4,300. Be sure to choose the answer choice most closely corresponding to the solution you’ve found.

Multiple Choice (Select One or More Answer Choices)

Want to improve your GRE score by 7 points? We have the industry's leading GRE prep program. Built by world-class instructors with 99th percentile GRE scores, the program learns your strengths and weaknesses through machine learning data science, then customizes your prep program to you so you get the most effective prep possible.
Try our 5-day full access trial for free:
The second type of multiple-choice question allows you to choose one or more answer choices. For these questions, the correct answer could be just a single answer choice, two of them, several of them, or all of them. ETS is unclear about how many of these questions we can expect, but we estimate there are about two or three multiple-answer questions per Quant section.
All answer choices for multiple-answer questions accompany square boxes instead of circles or ovals to indicate that you can select more than one answer. These questions can also contain fewer than five answer choices or more than five answer choices.
Lastly, some of these questions may instruct you to choose a certain number of answer choices (e.g., two or three) or all applicable answer choices (like the above example).
Numeric Entry

The final Quant question type is Numeric Entry. According to our estimates, there are about two Numeric Entry questions per Quant section.
Unlike the other question types, this is the only one that doesn’t supply you with answer choices. Instead, you must come up with your own answer and write it in the blank. Numeric Entry questions can ask for integers (i.e., whole numbers), decimals, or fractions (denoted by a numerator and denominator blank).
Before filling in an answer, note any special characters by the blank, such as a dollar sign ($), percent sign (%), etc. These symbols are helpful because they alert you to the type of solution you’ll need to find.
Additionally, be sure to round your answer appropriately. For example, if a Numeric Entry question asks for an integer and your answer is 67.89, write 68.
GRE Math: 110 Terms and Symbols You Must Know
The GRE expects all test takers to have a basic understanding of the math topics described above — and this includes both terms and symbols. Here are some of the most commonly encountered terms and symbols on Quant. (If you’d like to learn about GRE math formulas instead, check out our guide.) All terms are arranged alphabetically.
Terms
absolute value: the actual distance a number is from 0 on a number line
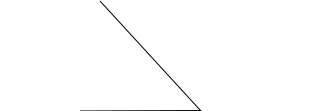
acute angle: any angle less than 90 degrees. Example:
algebraic expression: a mathematical expression with one or more variables, written as either a single term or a sum of terms. Example:
$$4x+8$$
angle: the shape formed by the convergence of two straight lines
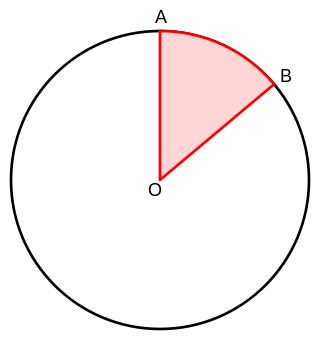
arc: all of the points located between two points on the edge of a circle. In the following example, AB is the arc:
area: the amount of space enclosed by a 2-D shape
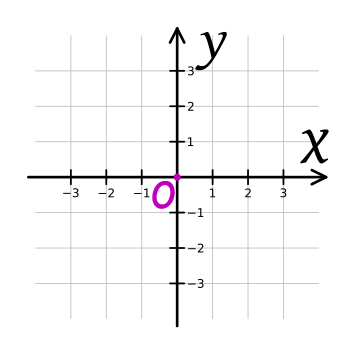
axis: the horizontal (x-axis) or vertical (y-axis) lines in a coordinate system, or a straight line joining the centers of the bases of a right circular cylinder. Example:
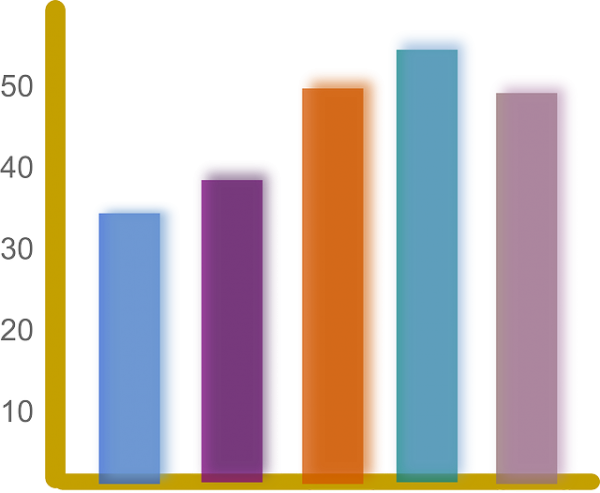
bar graph: a graph containing either horizontal or vertical bars with various heights corresponding to certain frequencies. Example:
base: a number being brought to a certain power with an exponent. For example, 4 is the base in $4^2$.
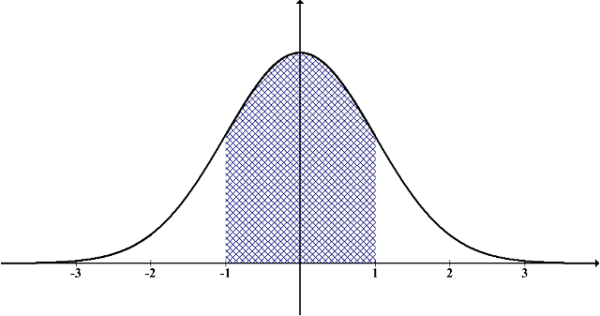
bell curve: a graph displaying a normal distribution (and thus creating a bell shape). Example:
central angle: a vertex located in the center of a circle and created by the intersection of two radii. See “arc” for diagram.
circle graph: a graph that represents data using the shape of a circle. Example:

circumference: the length around a circle (i.e., the perimeter of a circle)
coefficient: a number multiplied by a variable or variables. For example, 8 is the coefficient in $8x$.
combination: a way of selecting a certain number of things in which order is irrelevant
common denominator: a common multiple of two separate denominators. In the following example, 24 is a common denominator:
${2/3}:{5/8}={16/24}:{15/24}$
Want to improve your GRE score by 7+ points?
Check out our best-in-class online GRE prep program. We guarantee your money back if you don't improve your GRE score by 7 points or more.
PrepScholar GRE is entirely online, and it customizes your prep program to your strengths and weaknesses. We also feature 2,000 practice questions, official practice tests, 150 hours of interactive lessons, and 1-on-1 scoring and feedback on your AWA essays.
Check out our 5-day free trial now:
congruent: the same in shape or size
constant: a term with no variable. For example, 6 is a constant in $y=13x^2+5x-6$.
cross multiplication: a method for converting two equivalent fractions into products. Performed by multiplying both terms’ numerators by the other term’s denominators. Example:
$x/5=4/20$
$20x=20$
$x=1$
cube: a six-sided rectangular solid with the same length and width for all of its faces. Example:

denominator: the bottom number of a fraction. For example, 19 is the denominator in $10/19$.
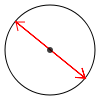
diameter: the length of a line cutting a circle in half and passing through the center point. Example:
dispersion: how far a set of data is spread out
divisor: the number you divide by in order to get a quotient. For example, 5 is the divisor in $50/5=10$.
equation: a mathematical statement depicting the equivalence of two different expressions. Example:
$y=12x+2$
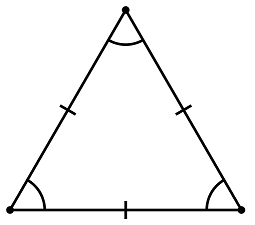
equilateral triangle: a triangle with three sides of the same length and three 45-degree angles. Example:
even integer: any whole number divisible by 2
exponent: a superscript number used to denote how many times a base is being multiplied by itself. For example, 6 is the exponent in $3^6=729$.
factor: a number multiplied to get a product. For example, 3 and 4 are both factors of 12 because $3*4=12$.
factorial: the product of all integers (until 1) less than and equal to a number. Example:
$3!=3*2*1=6$
fraction: a quantity that is not a whole number (written using a numerator and a denominator). Example:
$3/5$
frequency: the number of times a particular piece of data occurs
function: a mathematical relation between a set of possible inputs to a set of possible outputs
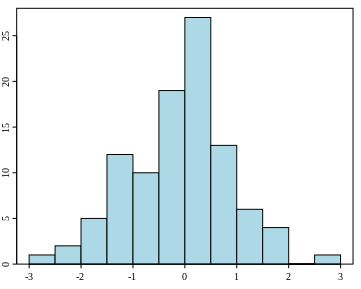
histogram: a type of graph depicting intervals and their frequencies. Example:
inequality: an expression signifying a relationship wherein two or more expressions are not equal to one another. Equal sign is replaced with >, <, or ≠. Example:
$x+y<8$
integer: any whole number (negative, positive, or 0)
irrational number: any number that cannot be represented as a ratio between two integers, or any number containing a never-ending, pattern-less decimal. Example:
$√{2}=1.41421356$ …
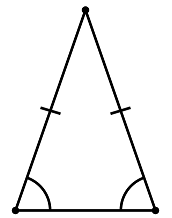
isosceles triangle: a triangle with two sides of the same length and two equal angles. Example:
least common multiple: the smallest number that is a multiple for two different values. For example, 6 is the least common multiple of 2 and 6 because $2*3=6$ and $1*6=6$.
linear equation: an equation that creates a straight line in a coordinate system. Example:
$y=5x+2$
mean: the average value of a data set (the sum of n numbers divided by n)
median: the middle value of a data set
mixed number: the combination of an integer and a fraction. Example:
$2{4/5}$
mode: the most common value of a data set
multiple: a possible product of an integer. For example, multiples of 4 include 4, 8, 12, 16, 20, etc.
normal distribution: a type of data distribution with a curved shape. See “bell curve” for diagram.
numerator: the top number of a fraction. For example, 3 is the numerator in $3/8$.
obtuse angle: any angle more than 90 degrees but less than 180 degrees. Example:
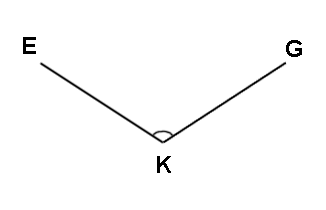
odd integer: any whole number not divisible by 2
origin: the center point of a coordinate system, or (0, 0). See “axis” for diagram.
outlier: a value in a data set that is distinctly separate (either extremely high or low) from the rest of the data
parabola: a curve in a coordinate system shaped like an arch. Example:
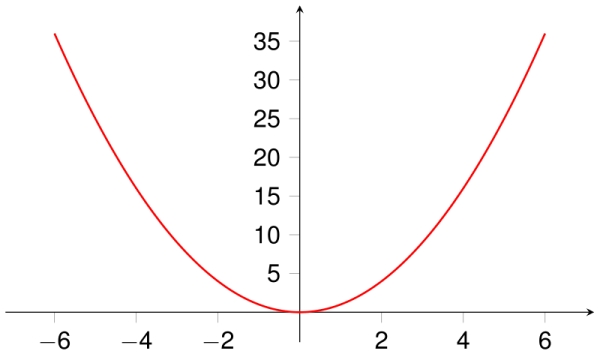
parallel lines: lines with the same slope and never intersecting. Example:

percent: parts per 100
perimeter: the length around a polygon (i.e., the sum of all sides)
permutation: a way of arranging a certain number of values in which order matters
perpendicular lines: lines that intersect to create only right angles. Example:
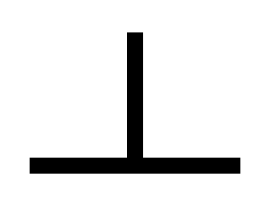
pi (π): a mathematical constant describing the ratio of a circle’s circumference to its diameter. Can be rounded to 3.14.
pie chart: see “circle graph”
polygon: a 2-D object made using straight lines. Examples:

prime number: any integer greater than 1 that can only be divided by 1 and itself. Examples include 2, 3, 5, 7, 11, 13, 17, 19, 23, etc. Note that 2 is the only even integer that is also a prime number.
probability: the likelihood of an event occurring
proportion: two equivalent terms displayed as a ratio
quadrilateral: any four-sided polygon, such as a square, rectangle, trapezoid, or parallelogram
quartile: one of four parts of a data set
radius: the length of a line extending from the center point of a circle to any point on the edge. Example:
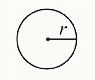
range: the difference between the highest and lowest values of a data set
ratio: a relationship between two numbers highlighting their relative values to each other. Example:
$2:7$
rational number: any number that can be represented as a ratio of two integers. Example:
$1/3$
real number: all rational and irrational numbers
reciprocal: any integer or fraction with its numerator and denominator switched (for reciprocals of integers, the numerator is 1). For example, $3/4$ is the reciprocal of $4/3$ and vice versa.
rectangular solid: any six-sided 3-D object. Example:
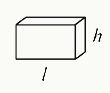
remainder: the leftover amount of a value after performing a computation (usually division)
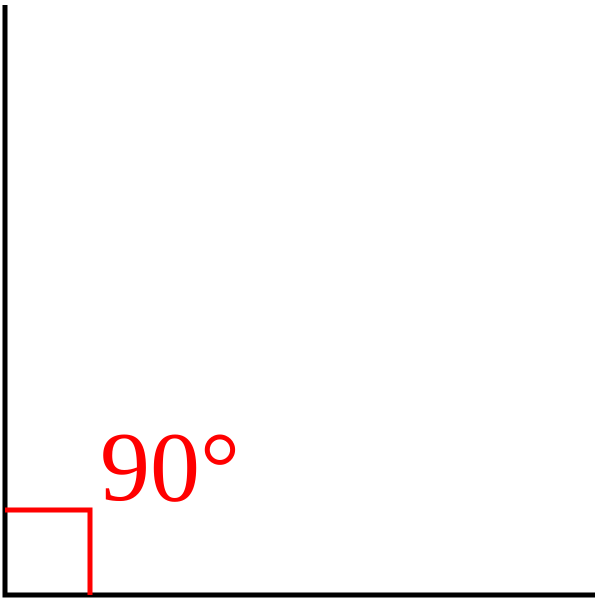
right angle: 90 degrees. Example:
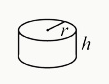
right circular cylinder: a 3-D object with two identical circular bases and an axis perpendicular to the bases’ center points. Example:
right triangle: a triangle with one 90-degree angle. The two shorter sides are the “legs” and the longest side (opposite the right angle) is the “hypotenuse.” Example:

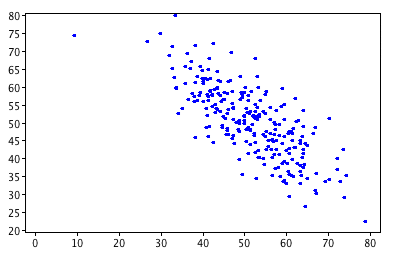
scatterplot: a type of graph depicting the relationship and trends of two separate variables. Example:
sector: the (shaded) region of a circle enclosed by an arc and two radii. See “arc” for diagram.
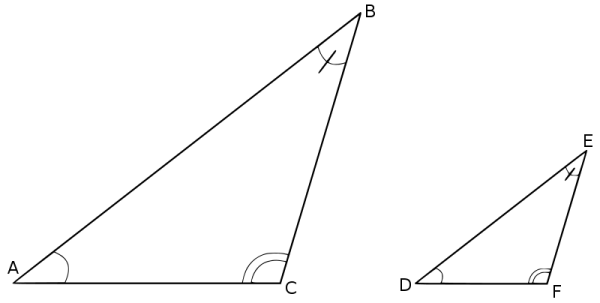
similar: the same in shape but not size. Example:
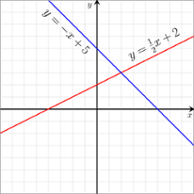
slope: the steepness of a line (in a coordinate system), represented by m in the equation $y=mx+b$. Lines with positive slopes increase from left to right, whereas lines with negative slopes decrease from left to right. Example:
solution: any value that solves an equation or inequality
square root: the number that produces a specific number when multiplied by itself. For example, 5 is the square root of 25, or $√{25}=5$.
standard deviation: a measure for how spread out a certain data set is
surface area: the total exterior area of a 3-D object
system of equations: a set of two or more equations with the same variables. Example:
$y=x+3$
$x=5-y$
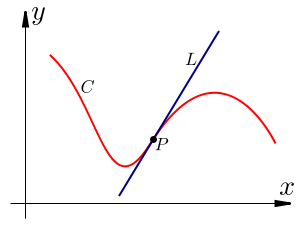
tangent: intersecting at precisely one point (on a shape). In the following example, curve C is tangent to line L at point P:
variable: an unknown quantity, usually represented by the letter x. For example, a is the variable in $5a-10=20$
vertex: the intersection of two straight lines, creating an angle
volume: the amount of space occupied by a 3-D object
x-axis: the horizontal reference line in a coordinate system. See “axis” for diagram.
x-coordinate: how far a point is horizontally from the origin of a coordinate system
x-intercept: where a line or shape passes through the x-axis
y-axis: the vertical reference line in a coordinate system. See “axis” for diagram.
y-coordinate: how far a point is vertically from the origin of a coordinate system
y-intercept: where a line or shape passes through the y-axis

Symbols
| Symbol | Meaning | Example |
| < | less than | 1 < 5 |
| > | greater than | 6 > 4 |
| ≤ | less than or equal to | x ≤ 10 |
| ≥ | greater than or equal to | x ≥ 3 |
| ≠ | does not equal | $1/2$ ≠ 0.75 |
| ≈ | approximately equal to | π ≈ 3.14 |
| ∥ | parallel to | A ∥ B |
| ⊥ | perpendicular to | C ⊥ D |
| ∠ | angle | ∠E |
| ° | degree (of an angle) | 73° |
| |a| | absolute value (of a number) | $|-4|=4$ |
| $√{a}$ | square root (of a number) | $√{100}=10$ |
| $ | dollar sign | $50.49 |
| % | percent | 26% |
| π | pi; can be rounded to 3.14 | $C=2πr$ |
| a! | factorial; the product of all integers from 1 to a | $4!=4*3*2*1=24$ |
GRE Math: 4 Helpful Tips for Studying
Unfortunately, skimming this GRE math review alone is likely not enough of a refresher for you to score highly on the GRE. Luckily, there are some strategies you can use while studying to ultimately help raise your GRE math score. Here are our top tips for acing Quant.
#1: Know the Fundamentals
You can’t expect to score highly on Quant if you’re completely unfamiliar with basic math concepts or if you haven’t practiced algebra and geometry in several years. This is why it’s important to know the fundamentals of all topics tested — that is, the basic rules, formulas, and concepts associated with arithmetic, algebra, geometry, and data analysis.
In the section above, I gave you a lengthy list of terms and symbols you’re bound to come across on the GRE. Memorizing these is key to understanding GRE math questions.
But the terms and symbols above are just a brief overview of the basics. Try to acquaint yourself even more with GRE math by using additional resources, such as our extensive guide for high-quality math practice.

#2: Memorize Formulas
In addition to reviewing fundamental math concepts, you should also memorize the most common GRE formulas. Formulas are often the one and only key to solving a particular Quant question. Unlike the SAT, you won’t get a handy list of formulas to start with! So memorize the formulas most likely to appear, such as the Pythagorean theorem and the circumference formula.
It’s also important you know in what situations you’re most likely to apply certain formulas. For example, if you’re dealing with a circle, you’ll probably need to use an area or circumference formula, not the Pythagorean theorem.
#3: Make Flashcards
Want a go-to study method? Look no further. Flashcards are an excellent way to drill specific concepts, especially GRE math topics.
For Quant, you can use flashcards to study math terms and symbols (such as those listed above), formulas, laws, shapes, and so on. I recommend you make your own set of flashcards, either with paper note cards or digital cards, so you can customize your study sessions by prioritizing concepts you’re less familiar with.
For tips on how to use the waterfall method with your flashcards, check out our article on GRE vocab. This guide specifically focuses on drilling vocab for GRE Verbal, but you can apply its overarching strategies to Quant prep, too.
#4: Drill Realistic Practice Questions
Memorizing concepts and formulas isn’t enough if you’re not actively testing what you know, so be sure to spend ample time drilling GRE-style questions. You’ll grow more accustomed to the types of questions you’ll face on Quant and can anticipate how certain concepts might be worded or presented to you.
Ideally, you’ll use official practice questions, as these are the ones most similar to what you’ll see on test day. High-quality GRE prep books, such as those created by Manhattan Prep or Princeton Review, also offer many realistic practice questions.
Be sure you’re testing yourself on a variety of math topics in the beginning so you can gauge what kinds of questions and concepts are most difficult for you. Then, shift your focus to drilling more challenging questions. Once you’re done drilling, test out what you’ve learned using full-length practice tests. As with practice questions, always prioritize official GRE practice tests over unofficial ones.

GRE Math Review: Takeaways
As you can see, there’s a lot you should know about GRE math before sitting for the exam.
To review, the Quantitative Reasoning section consists of two 35-minute, 20-question sections, which cover an array of math topics, namely algebra, arithmetic, geometry, and data analysis. Quant also uses a scoring scale of 130-170, on which 170 is a perfect score and 130 is the lowest possible score.
GRE math questions are presented in one of four ways:
- Quantitative Comparison: compare Quantity A and Quantity B and choose one of four answer choices
- Multiple choice (select one answer choice): choose one of five answer choices
- Multiple choice (select one or more answer choices): choose one, two, several, or all answer choices
- Numeric Entry: write your answer in the blank(s) provided
And finally, here are our top four tips for studying Quant:
- Know the fundamental rules and laws of algebra, arithmetic, geometry, and data analysis
- Memorize common GRE formulas
- Study with flashcards
- Practice with GRE-style questions, prep books, and official practice tests
Quant is just a single part of your GRE score. But as this GRE math review emphasizes, it is nevertheless an important part that shouldn’t be approached haphazardly. In the end, you should know exactly what kind of math is on the GRE, be able to recall all of the major concepts and strategies, and have the confidence that you, too, can get a great score on Quant!
What’s Next?
Do you dream of acing Quant? Then take a look at our guides on how to maximize your GRE score and how to get a perfect Quant score. In addition, learn how to set a Quant goal score using my step-by-step guide.
Want additional GRE resources? Use our compilation of the top resources for GRE math practice to sharpen your math skills, and sneak a peek at some of the best GRE prep books currently available!
Still need to get started? Don’t dawdle! Just follow our easy guide to GRE registration. And for additional questions, check out our comprehensive GRE FAQ.
Ready to improve your GRE score by 7 points?
We've written a eBook about the top 5 strategies you must be using to have a shot at improving your GRE score.
Download it for free now:

