
You can’t claim to be ready for the GRE if you don’t know the ins and outs of Quantitative Comparison questions. This type of question, also known as “Quant Comp,” plays a critical role on the Quantitative Reasoning section, accounting for approximately 38 percent of all math questions. That’s more than a third of your overall Quant score!
But what exactly are you being tested on with these questions? And are there any tips for approaching them on the GRE? In this article, we’ll explore the function and purpose of Quantitative Comparisons. We’ll also give you advice on how to study and successfully tackle Quantitative Comparison questions on test day.
What Are Quantitative Comparison Questions?
First things first: what are Quantitative Comparison questions and how critical of a role do they play on the GRE?
There are two Quantitative Reasoning sections on the GRE. Each section contains 20 questions, of which seven to eight are Quantitative Comparisons. (In addition to Quantitative Comparisons, Quant consists of multiple choice and Numeric Entry questions.) Every test taker will have a grand total of about 15 Quantitative Comparisons while taking the GRE. Clearly, Quantitative Comparisons make up a significant portion of the exam (not to mention your Quant score)!
Now, onto what they are. All Quantitative Comparisons consist of two quantities (Quantity A and Quantity B), which are usually accompanied by a description, such as a diagram, a pair of coordinates, an equation, or a couple of sentences describing a major rule or relationship. Your task is to compare the two quantities and select one of four possible answer choices:
- Quantity A is greater.
- Quantity B is greater.
- The two quantities are equal.
- The relationship cannot be determined from the information given.
Quantitative Comparisons cover a wide array of topics, including arithmetic, algebra, geometry, and data analysis. But the answer choices above are the same answer choices for all Quantitative Comparison questions, regardless of the type of math they’re testing. So there’s no need to worry about any sudden changes or curve balls. This is actually one of the few times the GRE isn’t actively trying to trick you (yippee!).
These are the basics of Quantitative Comparisons. But what are some specific strategies you can use when facing these questions on test day?
Quick side note: we've created the world's leading online GRE prep program that adapts to you and your strengths and weaknesses. Not sure what to study? Confused by how to improve your score? We give you minute by minute guide.
You don't NEED a prep program to get a great GRE score. But we believe PrepScholar is the best GRE prep program available right now, especially if you find it hard to organize your study schedule and don't know what to study.
Click here to learn how you can improve your GRE score by 7 points, guaranteed.

5 Tips for GRE Quantitative Comparison Questions
Quantitative Comparisons can be tricky for first-time GRE takers, but they’re certainly not unbeatable. Here are our top five tips for approaching (and solving!) GRE Quantitative Comparison questions.
#1: Identify the Type of Math Being Tested
As soon as you encounter a Quantitative Comparison question on the GRE, try to pinpoint the exact topic it’s testing you on (e.g., geometry, algebra, etc.). Being aware of the type of math you’re dealing with allows you to anticipate what sorts of rules, formulas, or strategies you might be able to apply to a particular problem.
For example, with a Quantitative Comparison question focusing on data analysis, you’ll likely have to solve for means, medians, modes, and other statistical concepts. Likewise, if you encounter a pair of shapes, you can expect to have to calculate areas, perimeters, circumferences, etc.
In order to identify the type of math being tested, you’ll have to have a rough idea of how different types of math are normally presented in Quantitative Comparison questions on the GRE. Typically, geometry questions contain diagrams of shapes; algebra questions contain equations and inequalities; and data analysis questions contain tables and graphs.
To illustrate this idea more clearly, take a look at the following example:
Because of the presence of a histogram, we can immediately recognize this problem as a data analysis question — specifically, one testing us on our knowledge of standard deviations and distribution.
But not all Quantitative Comparison questions are as obvious as this one. Some offer minimal info without any graphs, diagrams, or algebraic expressions to refer to. These bare-bones questions look something like this:

Unlike our previous example, this Quantitative Comparison contains neither a graph nor a description; all it offers are quantities. But don’t make the mistake of assuming all questions centering on a certain math concept will appear the same on the GRE. Why? Because this question is a data analysis question, too!
Confused? Take a closer look at the quantities in our examples above. Both questions are asking you to compare standard deviations — a telltale indicator that each of the problems is focusing on data.
If you’re ever stuck on a Quantitative Comparison question, look for keywords in the description (if present) and quantities to help you determine the topic being tested. Keywords are any major terms commonly associated with certain fields of math, such as the names of shapes (for geometry) or the words “slope” and “variable” (for algebra).

#2: Determine Whether Any Rules or Formulas Are at Play
Another step to take before attempting to solve a Quantitative Comparison is to determine whether there are any rules or formulas you’ll need in order to solve the problem.
In reality, many Quantitative Comparison questions can only be solved through the application of a law or formula. For example, if you can’t recall the circumference formula, you’ll be unable to solve a Quantitative Comparison asking you to compare the circumferences of two separate circles.
Most of the major rules you need for Quant are covered in our guide to the top GRE math formulas and our comprehensive geometry review. To reiterate briefly, though, here is an overview of some of the most important math concepts you should know:
- PEMDAS (the order of operations)
- Relationships between even and odd numbers
- How to simplify and combine values containing exponents or square roots
- How to simplify algebraic expressions
- How to interpret graphs, charts, and tables
- How to graph functions and lines on coordinate systems
- How to calculate probability and percentages
- Rules of geometry, including lines, shapes, and angles
Now, let’s look at an example of how knowing a single rule can assist you in solving a Quantitative Comparison:
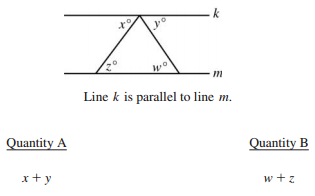

Just by glancing at the diagram, you should be able to identify the problem as a geometry question involving angles. Now, look at the quantities. We’re being asked to compare the sums of two sets of angles, but we’re given no specific values for any of the angles. Thus, we’ll have to rely on our knowledge of the rules of angles — specifically, the rules of angles created by a line intersecting two parallel lines.
Allow me to explain what I mean by this. The problem above states that lines k and m are parallel to each other. (Never assume two lines are parallel unless clearly indicated.) Two lines are intersecting k and m in a triangular shape to create a total of seven angles. Four of these angles are given degree measurements of x, y, z, and w. As geometry problems are not drawn to scale on the GRE, we cannot make any assumptions about the measurements of these angles.
So how are we supposed to compare the sums of the angles? By applying the rule of alternate interior angles.
Look at the first intersecting line (the one making angles measuring x and z degrees). Because lines k and m are parallel to each other, the angles for x and z are therefore alternate interior angles. According to the rules of geometry, alternate interior angles are always equal in measure, so $x=z$.
Now, look at the other intersecting line (the one making angles measuring y and w degrees). The angles for y and w are in similar positions as x and z and are therefore also alternate interior angles, so $y=w$.
Because $x=z$ and $y=w$, Quantities A and B are essentially combining the same values and will therefore produce equivalent sums. The correct answer is C: The two quantities are equal.

In addition to rules, you should also attempt to memorize common formulas, primarily those for:
- Perimeter
- Area
- Circumference
- Volume
- Surface area
- Slope
Here is an example of a Quantitative Comparison question requiring knowledge of a particular formula:
Want to improve your GRE score by 7 points? We have the industry's leading GRE prep program. Built by world-class instructors with 99th percentile GRE scores, the program learns your strengths and weaknesses through machine learning data science, then customizes your prep program to you so you get the most effective prep possible.
Try our 5-day full access trial for free:

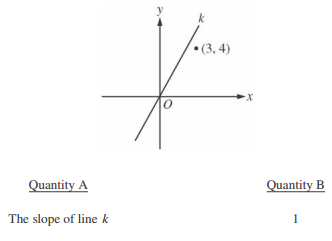
In this question, we’re being asked to compare the slope of line k to Quantity B (1). Thus, in order to compare the two quantities, we must know how to find a slope using the slope formula.
There are two slope formulas we can use: the equation for a line ($y=mx+b$), wherein m is the slope of the line, and the formula for a slope (also called the “rise over run”). Because we want to solve for the slope of line k, it’ll be faster for us to use the rise-over-run formula, which states:
$$m={y_2-y_1}/{x_2-x_1}$$
To use this formula, we must first identify two sets of coordinates on our line. Start by looking at the coordinate system above. Because the line passes straight through the center point of the plane, one of our points is, for certain, (0, 0).
But we need another set of coordinates to be able to use the formula. The point (3, 4) is close to our line, so let’s use it to estimate a point on our line. (Coordinate systems are drawn to scale on the GRE, so it’s OK to estimate coordinates.) Below is the same coordinate system marked with one-point increments to help us make a more precise estimate:
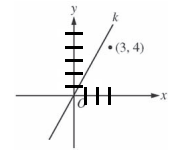
According to our estimates, our line has possible points around (2, 4) and (3, 5). You can work with either of these estimated sets of coordinates. Now, just plug in whatever coordinates you’ve chosen along with our exact coordinates, (0, 0), and solve for the slope of line k:
Using (2, 4): $m={4-0}/{2-0}$
$m=4/2$
$m=2$
Using (3, 5): $m={5-0}/{3-0}$
$m=5/3$
$m=1.67$
According to our calculations, the slope of line k is somewhere around 1.67 or 2. Both of these numbers are larger than 1, so the correct choice is A: Quantity A is greater.
#3: Plug In Numbers
A popular method for solving algebraic expressions in Quantitative Comparison questions is plugging in numbers. If you’re only given a single value to work with, such as x, it’s imperative you plug in at least two different numbers to see if the result remains consistent for both cases. If not, the correct answer will be “D: The relationship cannot be determined from the information given.”
Generally, it’s best to choose a pair of numbers that differ greatly from each other, such as a positive number and a negative number, a small number and a large number (i.e., two extremes), 0 and a non-zero number, etc.
Often, expressions work consistently for closely connected values but won’t work at all for rare or special values, such as 0, negative numbers, and fractions. As a result, these are good numbers to choose when testing an expression or equation.
Here’s an example:
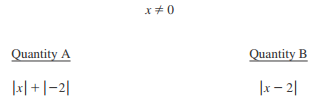

According to this Quantitative Comparison, x cannot equal 0 (but can equal a negative or positive number). Because we aren’t given an exact value for x, let’s try plugging in a combination of positive and negative numbers to see how they affect the quantities.
But before we start choosing values, look at Quantity A. The absolute value of -2 is always 2, so let’s rewrite this expression more simply as $|x|+2$.
Now, it’s time to plug in some numbers. Let’s say $x=1$ and apply this scenario to both of our quantities:
Quantity A: $|1|+2$
$1+2=3$
Quantity B: $|1-2|$
$|-1|=1$
In this case, Quantity A (3) is larger than Quantity B (1). But before we mark choice A as our answer, let’s plug in a different number and see if it changes (or validates) our result. We’ve already tested a positive number, so let’s try a negative one. Here’s what happens to both of the expressions when $x=-1$:
Quantity A: $|-1|+2$
$1+2=3$
Quantity B: $|-1-2|$
$|-3|=3$
In this scenario, the two quantities both come out to 3 and are therefore equal.
But this isn’t the same result we initially got. When $x=1$ Quantity A is greater than Quantity B, but when $x=-1$ the two quantities are equal. Therefore, the correct answer is D: The relationship cannot be determined from the information given.
Want to improve your GRE score by 7+ points?
Check out our best-in-class online GRE prep program. We guarantee your money back if you don't improve your GRE score by 7 points or more.
PrepScholar GRE is entirely online, and it customizes your prep program to your strengths and weaknesses. We also feature 2,000 practice questions, official practice tests, 150 hours of interactive lessons, and 1-on-1 scoring and feedback on your AWA essays.
Check out our 5-day free trial now:

#4: Simplify Algebraic Expressions
Although a convenient strategy, plugging in numbers isn’t always necessary if you can simplify the algebraic expressions and compare the two quantities as is. This can only be done if both quantities contain the same variables.
Let’s look at an example of how we could do this on the GRE:
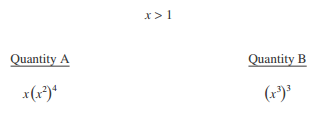

This Quantitative Comparison is clearly an algebraic one revolving around the variable x. We know $x>1$ but have no idea what the value of x actually is, so let’s look at the two quantities for a moment. Because both contain the same variable and are written using exponents, we should be able to compare them using the laws of exponents.
One of the rules of exponents states:
$$(x^a)^b=x^{ab}$$
In other words, a base raised to the power of a and subsequently raised to the power of b is equal to the same base raised to the power of ab. If we apply this rule to Quantity B, we get:
$(x^3)^3=x^9$
Now, let’s apply the rule to Quantity A:
$x(x^2)^4$
$x(x^8)$
Clearly, we’re not finished, yet. We have another x to multiply this expression by — meaning, all we have to do is add 1 to the current exponent. Not following me? Imagine $x^8$ written out as such:
$$x*x*x*x*x*x*x*x$$
As you can see, $x^8$ is just eight x’s multiplied together. If we were to multiply this expression by another x, we’d have nine x’s, or $x^9$.
In the end, Quantity A simplifies to $x^9$ and Quantity B also simplifies to $x^9$. The answer is C: The two quantities are equal.
#5: Draw a Diagram
Drawing a diagram is an especially helpful method when faced with a Quantitative Comparison centering on geometry. By drawing the shapes described in a problem, you’ll be better able to understand the relationships among values and won’t lose track of what formula or rule you need to focus on.
Here’s an example of a Quantitative Comparison you can (and should) draw a diagram for:


For this question, it’s difficult to visualize where the substations and power station could be in or along a square because there are so many individual points to keep track of. Let’s start by drawing a simple diagram (not drawn to scale). The problem describes a square region with lengths of 10 miles on each side:
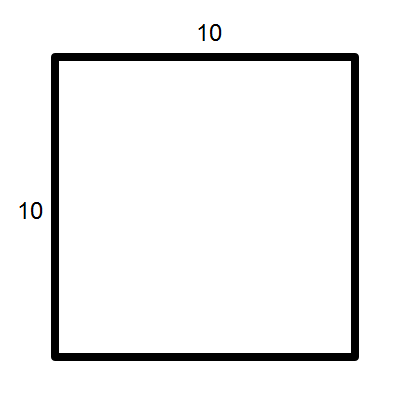
What we know for sure is this: the power station is located somewhere along the perimeter of the square, and the three substations are located somewhere inside the square.
Now, let’s “plug in” potential locations for the four stations. To get a large sum of distances, we’ll need all of the substations situated far away from the power station. The farthest you can get in a square is directly opposite a corner — i.e., the hypotenuse of a right triangle diagonally dividing the square in half. Here’s how this would look, with c representing the length of the hypotenuse:
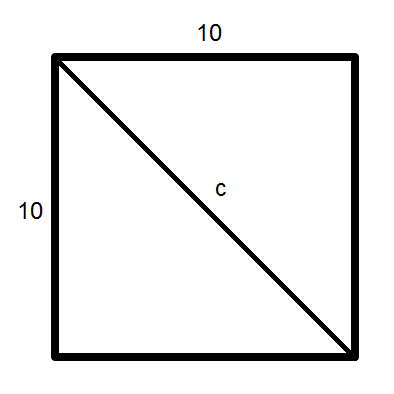
To solve for c, we must use the Pythagorean theorem, or $a^2+b^2=c^2$. In this case, the “legs” of the triangle are equivalent to the sides of the square. So, a and b both equal 10 and can be plugged in as so:
$10^2+10^2=c^2$
$100+100=c^2$
$200=c^2$
$√{200}=c$
$c=14.14$
According to our calculations, the largest possible distance (from one corner to an opposite corner) is about 14.14 miles. Now, let’s choose a couple of possible locations for our stations. First, let’s create a large distance by placing all three substations far away from the power station. The red dot is the power station, and the three blue dots are the substations:
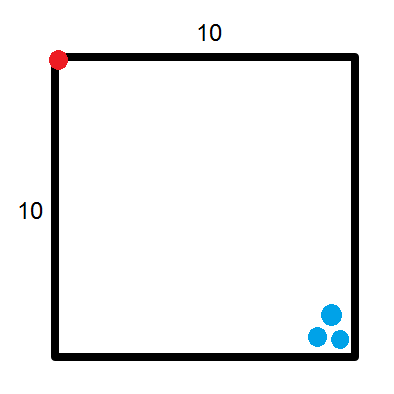
In this example, all three substations are around 14 miles away from the power station (their distances are slightly less than 14 as they cannot be placed directly on the corner). Let’s say their distances from the power station are 14, 13, and 12.5 miles, respectively. By adding these numbers together, we get a total of 39.5 miles, which is more than 30 miles. So, in this scenario, Quantity A is greater than Quantity B.
But let’s try another arrangement before choosing an answer choice. This time, we’ll place the three substations extremely close to the power station:
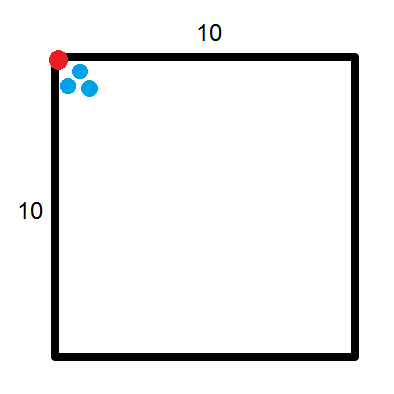
Let’s say their distances from the power station are 1, 2, and 2.5 miles, respectively. Altogether, this distance equals only 5.5 miles — significantly less than the 30 miles listed for Quantity B.
In other words, in one scenario Quantity A is greater than Quantity B, and in another scenario the opposite is true. The correct answer, therefore, is D: The relationship cannot be determined from the information given.

GRE Quantitative Comparison Practice: 3 Study Tips
Because Quantitative Comparison questions are such a large part of Quant, it’s important you give ample attention to these types of questions in your study sessions. Below are some of our top tips for effectively studying Quantitative Comparisons.
#1: Memorize the Answer Choices
With only 35 minutes for each Quant section, you’ll have to limit the time you spend on each math question. You can, therefore, decrease the time it takes you to answer Quantitative Comparison questions by memorizing the four answer choices ahead of time:

Remember, these answer choices are the same for all Quantitative Comparison questions, no matter what type of math is being tested.
A and B are the easiest to remember because A corresponds to Quantity A’s being greater, and B corresponds to Quantity B’s being greater. You can think of C as being short for “congruent,” meaning “the same.” And you can associate D with the word “determined” to remind you that D “cannot be determined.”
You’ll always be directly given the answer choices for Quantitative Comparisons, but not having to pore over each answer choice individually should save you at least a couple of seconds for each question.
#2: Focus on Algebra
There’s no telling exactly what types of Quantitative Comparison questions you’ll get on the exam. But based on our estimates, algebra appears to be a favorite subject of Quantitative Comparisons. In algebra-based questions, the two quantities being compared are usually:
- Two algebraic expressions
- Two variables
- One algebraic expression and one number
- One variable and one number
Furthermore, most algebraic Quantitative Comparison questions deal with one or more of the following concepts:
- (Systems of) inequalities
- (Systems of) equations
- Lines
- Slopes
This isn’t to say you should simply forgo studying geometry, arithmetic, and data analysis; these topics are commonly tested, too. Just know, however, that Quantitative Comparisons expect you to be most familiar with algebra.

#3: Use High-Quality Study Materials
The best way to study for the GRE in general is to use reliable prep materials, or those that test you on concepts and question types similar to what’s on the actual test.
More specifically, use your study materials to practice Quantitative Comparisons and to gauge what topics are easy or challenging for you. For example, if you’re struggling to understand algebraic Quantitative Comparisons, use your prep books to review basic algebra concepts and drill GRE-like questions.
Always opt for official materials, as they offer Quantitative Comparison practice most similar to those you’ll encounter on test day. Check out our articles for more info on the top GRE prep books you can use and the best resources currently available for GRE math practice.
You can also test out your Quantitative Comparison skills using official practice tests. At present, ETS offers six official practice tests free of charge. With these tests, be sure to imitate a real GRE setting as closely as possible by giving yourself ample scratch paper ahead of time and finding a quiet area to take the test.
Review: How to Approach GRE Quantitative Comparison Questions
Quantitative Comparison questions account for more than a third of GRE Quant. Therefore, it’s important you familiarize yourself with the types of math these questions test in addition to how they’re likely to be tested.
Our top tips for approaching a Quantitative Comparison on the GRE are to:
- Identify the type of math being tested
- Figure out what, if any, rules or formulas are at play
- Plug in numbers
- Simplify algebraic expressions if the two quantities being compared contain the same variables
- Draw a diagram
When it comes to studying for Quantitative Comparison questions, be sure you:
- Memorize the four possible answer choices
- Focus on algebra
- Use premier study materials, including prep books and free official practice tests
Hopefully, you now have a little more confidence when it comes to tackling Quantitative Comparison questions on the GRE!
What’s Next?
Looking for more Quant resources? Check out our in-depth guide to the most important GRE math formulas you should know, and explore our expert picks for the best resources for GRE Quant practice.
Ready to raise your Quant score? Learn everything you need to know about getting a high math score with our articles on what a good Quant score is and how to ace Quant.
In need of some test-day tips for Quant? Get advice on how to use the on-screen calculator and read our strategies for using your scratch paper.
Ready to improve your GRE score by 7 points?
We've written a eBook about the top 5 strategies you must be using to have a shot at improving your GRE score.
Download it for free now:
